# 减小DOM操作的性能开销
上一章我们讨论了渲染器是如何更新各种类型的 VNode 的,实际上,上一章所讲解的内容归属于完整的 Diff 算法之内,但并不包含核心的 Diff 算法。那什么才是核心的 Diff 算法呢?看下图:
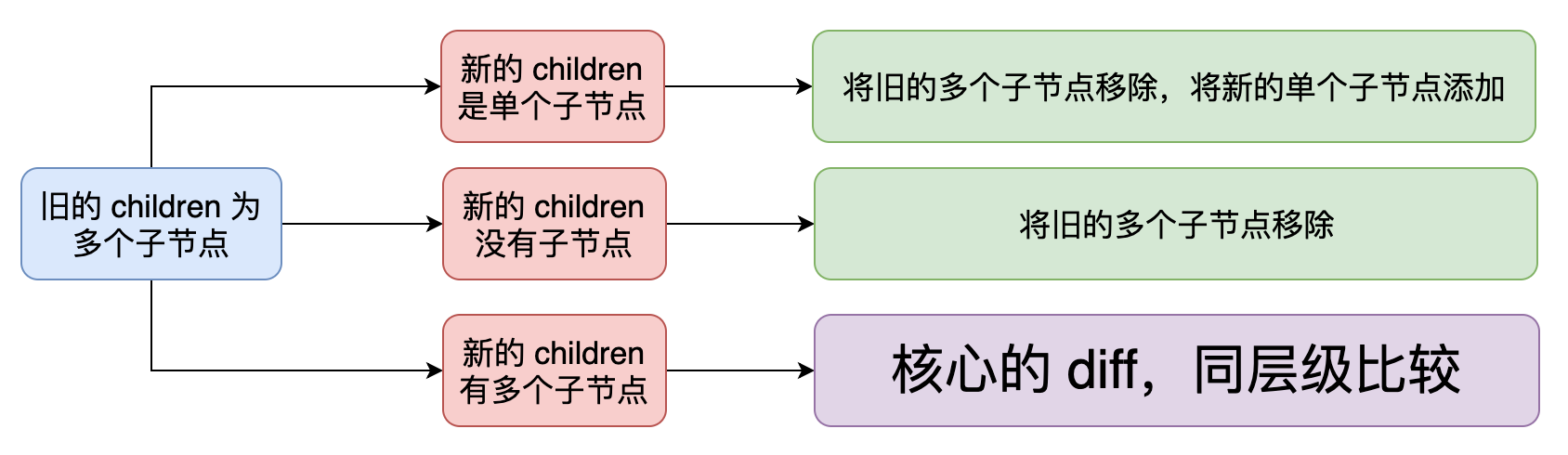
我们曾在上一章中讲解子节点更新的时候见到过这张图,当时我们提到只有当新旧子节点的类型都是多个子节点时,核心 Diff 算法才派得上用场,并且当时我们采用了一种仅能实现目标但并不完美的算法:遍历旧的子节点,将其全部移除;再遍历新的子节点,将其全部添加,如下高亮代码所示:
function patchChildren(
prevChildFlags,
nextChildFlags,
prevChildren,
nextChildren,
container
) {
switch (prevChildFlags) {
// 省略...
// 旧的 children 中有多个子节点
default:
switch (nextChildFlags) {
case ChildrenFlags.SINGLE_VNODE:
// 省略...
case ChildrenFlags.NO_CHILDREN:
// 省略...
default:
// 新的 children 中有多个子节点
// 遍历旧的子节点,将其全部移除
for (let i = 0; i < prevChildren.length; i++) {
container.removeChild(prevChildren[i].el)
}
// 遍历新的子节点,将其全部添加
for (let i = 0; i < nextChildren.length; i++) {
mount(nextChildren[i], container)
}
break
}
break
}
}
为了便于表述,我们把这个算法称为:简单 Diff 算法。简单 Diff 算法虽然能够达到目的,但并非最佳处理方式。我们经常会遇到可排序的列表,假设我们有一个由 li 标签组成的列表:
<ul>
<li>1</li>
<li>2</li>
<li>3</li>
</ul>
列表中的 li 标签是 ul 标签的子节点,我们可以使用下面的数组来表示 ul 标签的 children:
[
h('li', null, 1),
h('li', null, 2),
h('li', null, 3)
]
接着由于数据变化导致了列表的顺序发生了变化,新的列表顺序如下:
[
h('li', null, 3),
h('li', null, 1),
h('li', null, 2)
]
新的列表和旧的列表构成了新旧 children,当我们使用简单 Diff 算法更新这两个列表时,其操作行为可以用下图表示:
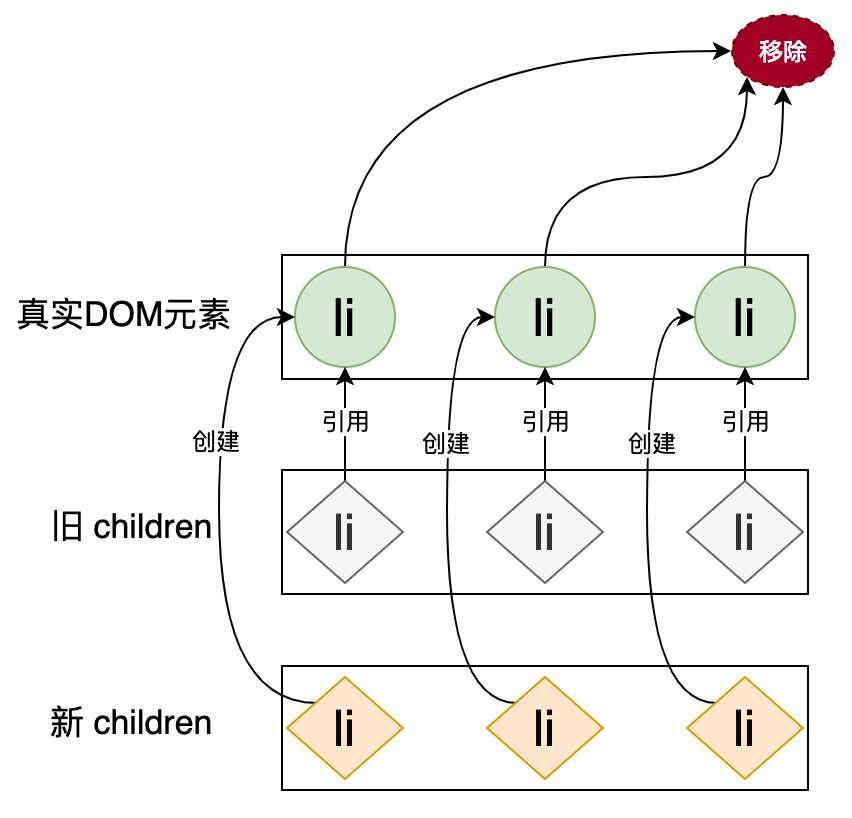
在这张图中我们使用圆形表示真实 DOM 元素,用菱形表示 VNode,旧的 VNode 保存着对真实 DOM 的引用(即 vnode.el 属性),新的 VNode 是不存在对真实 DOM 的引用的。上图描述了简单 Diff 算法的操作行为,首先遍历旧的 VNode,通过旧 VNode 对真实 DOM 的引用取得真实 DOM,即可将已渲染的 DOM 移除。接着遍历新的 VNode 并将其全部添加到页面中。
在这个过程中我们能够注意到:更新前后的真实 DOM 元素都是 li 标签。那么可不可以复用 li 标签呢?这样就能减少“移除”和“新建” DOM 元素带来的性能开销,实际上是可以的,我们在讲解 pathcElement 函数时了解到,当新旧 VNode 所描述的是相同标签时,那么这两个 VNode 之间的差异就仅存在于 VNodeData 和 children 上,所以我们完全可以通过遍历新旧 VNode,并一一比对它们,这样对于任何一个 DOM 元素来说,由于它们都是相同的标签,所以更新的过程是不会“移除”和“新建”任何 DOM 元素的,而是复用已有 DOM 元素,需要更新的只有 VNodeData 和 children。优化后的更新操作可以用下图表示:
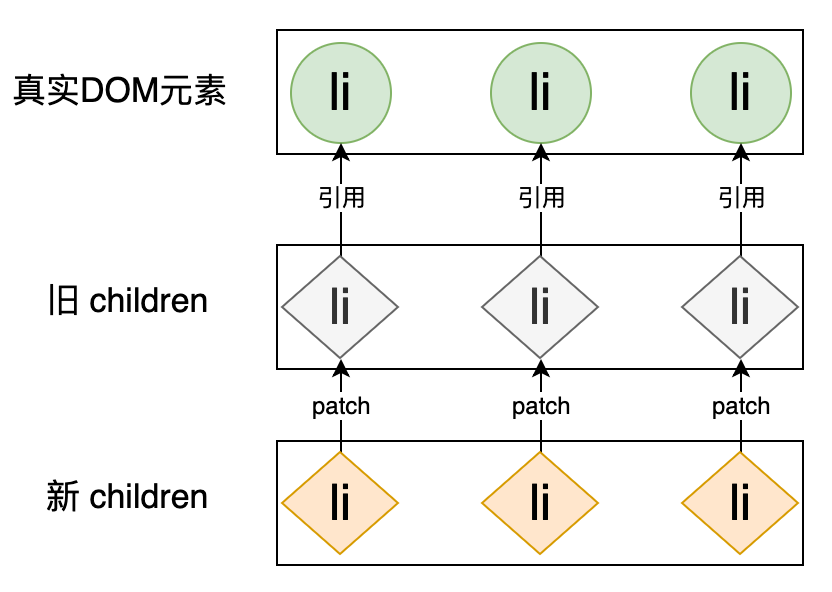
用代码实现起来也非常简单,如下高亮代码所示:
function patchChildren(
prevChildFlags,
nextChildFlags,
prevChildren,
nextChildren,
container
) {
switch (prevChildFlags) {
// 省略...
// 旧的 children 中有多个子节点
default:
switch (nextChildFlags) {
case ChildrenFlags.SINGLE_VNODE:
// 省略...
case ChildrenFlags.NO_CHILDREN:
// 省略...
default:
for (let i = 0; i < prevChildren.length; i++) {
patch(prevChildren[i], nextChildren[i], container)
}
break
}
break
}
}
通过遍历旧的 children,将新旧 children 中相同位置的节点拿出来作为一对“新旧 VNode”,并调用 patch 函数更新之。由于新旧列表的标签相同,所以这种更新方案较之前相比,省去了“移除”和“新建” DOM 元素的性能开销。而且从实现上看,代码也较之前少了一些,真可谓一举两得。但不要高兴的太早,细心的同学可能已经发现问题所在了,如上代码中我们遍历的是旧的 children,如果新旧 children 的长度相同的话,则这段代码可以正常工作,但是一旦新旧 children 的长度不同,这段代码就不能正常工作了,如下图所示:
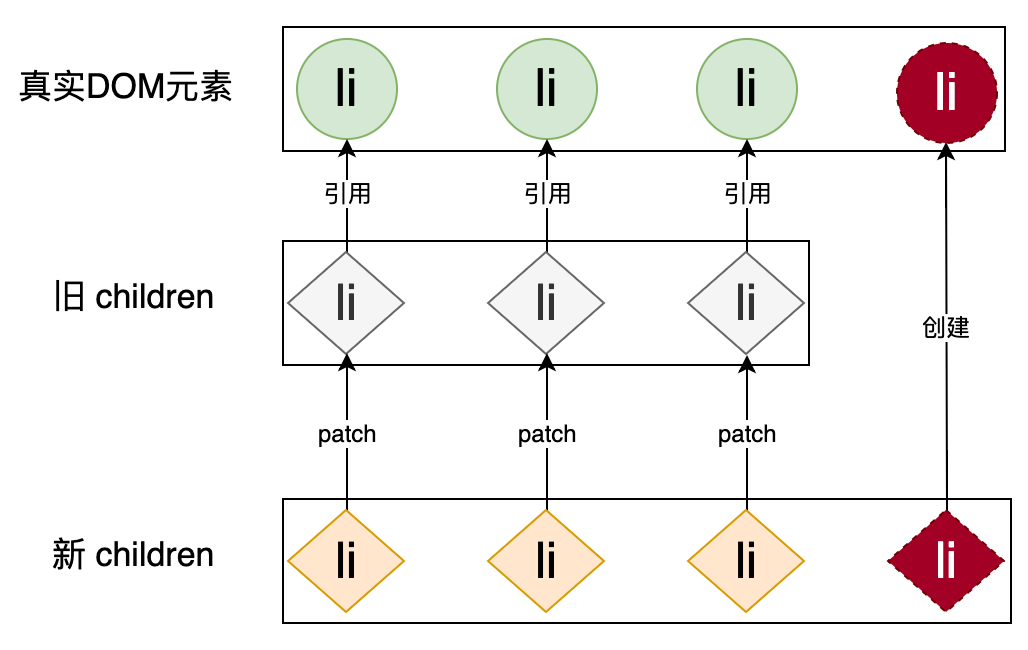
当新的 children 比旧的 children 的长度要长时,多出来的子节点是没办法应用 patch 函数的,此时我们应该把多出来的子节点作为新的节点添加上去。类似的,如果新的 children 比旧的 children 的长度要短时,我们应该把旧的 children 中多出来的子节点移除,如下图所示:
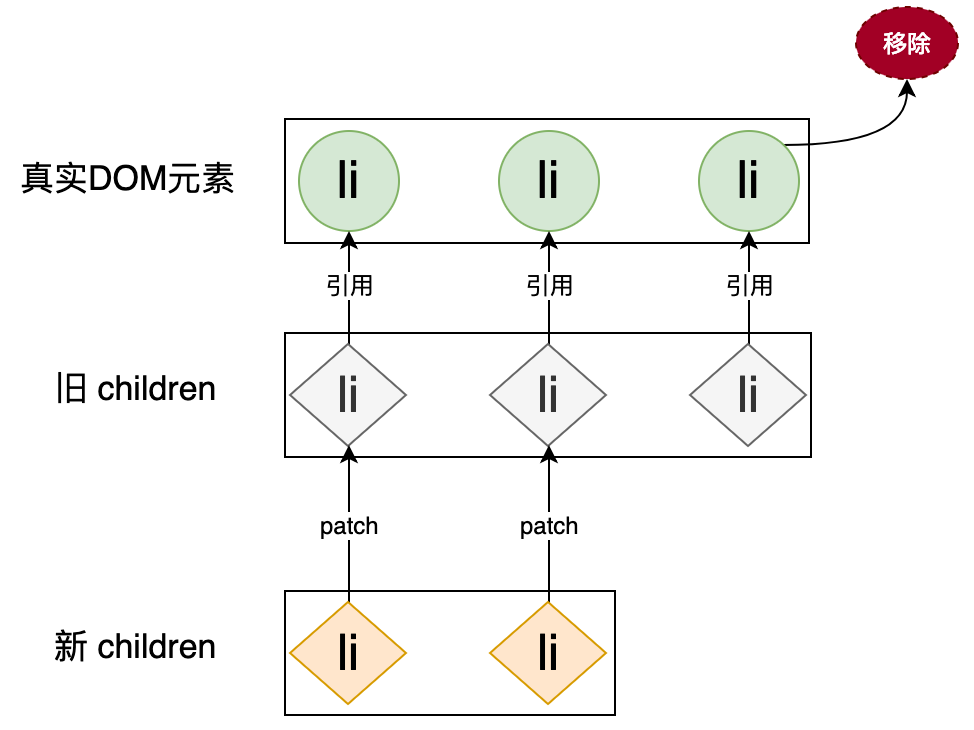
通过分析我们得出一个规律,我们不应该总是遍历旧的 children,而是应该遍历新旧 children 中长度较短的那一个,这样我们能够做到尽可能多的应用 patch 函数进行更新,然后再对比新旧 children 的长度,如果新的 children 更长,则说明有新的节点需要添加,否则说明有旧的节点需要移除。最终我们得到如下实现:
function patchChildren(
prevChildFlags,
nextChildFlags,
prevChildren,
nextChildren,
container
) {
switch (prevChildFlags) {
// 省略...
// 旧的 children 中有多个子节点
default:
switch (nextChildFlags) {
case ChildrenFlags.SINGLE_VNODE:
// 省略...
case ChildrenFlags.NO_CHILDREN:
// 省略...
default:
// 新的 children 中有多个子节点
// 获取公共长度,取新旧 children 长度较小的那一个
const prevLen = prevChildren.length
const nextLen = nextChildren.length
const commonLength = prevLen > nextLen ? nextLen : prevLen
for (let i = 0; i < commonLength; i++) {
patch(prevChildren[i], nextChildren[i], container)
}
// 如果 nextLen > prevLen,将多出来的元素添加
if (nextLen > prevLen) {
for (let i = commonLength; i < nextLen; i++) {
mount(nextChildren[i], container)
}
} else if (prevLen > nextLen) {
// 如果 prevLen > nextLen,将多出来的元素移除
for (let i = commonLength; i < prevLen; i++) {
container.removeChild(prevChildren[i].el)
}
}
break
}
break
}
}
TIP
完整代码&在线体验地址:https://codesandbox.io/s/qqxxlxzwm6 (opens new window)
实际上,这个算法就是在没有 key 时所采用的算法,该算法是存在优化空间的,下面我们将分析如何进一步优化。
# 尽可能的复用 DOM 元素
# key 的作用
在上一小节中,我们通过减少 DOM 操作的次数使得更新的性能得到了提升,但它仍然存在可优化的空间,要明白如何优化,那首先我们需要知道问题出在哪里。还是拿上一节的例子来说,假设旧的 children 如下:
[
h('li', null, 1),
h('li', null, 2),
h('li', null, 3)
]
新的 children 如下:
[
h('li', null, 3),
h('li', null, 1),
h('li', null, 2)
]
我们来看一下,如果使用前面讲解的 Diff 算法来更新这对新旧 children 的话,会进行哪些操作:首先,旧 children 的第一个节点和新 children 的第一个节点进行比对(patch),即:
h('li', null, 1)
// vs
h('li', null, 3)
patch 函数知道它们是相同的标签,所以只会更新 VNodeData 和子节点,由于这两个标签都没有 VNodeData,所以只需要更新它们的子节点,旧的 li 元素的子节点是文本节点 '1',而新的 li 标签的子节点是文本节点 '3',所以最终会调用一次 patchText 函数将 li 标签的文本子节点由 '1' 更新为 '3'。接着,使用旧 children 的第二个节点和新 children 的第二个节点进行比对,结果同样是调用一次 patchText 函数用以更新 li 标签的文本子节点。类似的,对于新旧 children 的第三个节点同样也会调用一次 patchText 函数更新其文本子节点。而这,就是问题所在,实际上我们通过观察新旧 children 可以很容易的发现:新旧 children 中的节点只有顺序是不同的,所以最佳的操作应该是通过移动元素的位置来达到更新的目的。
既然移动元素是最佳期望,那么我们就需要思考一下,能否通过移动元素来完成更新?能够移动元素的关键在于:我们需要在新旧 children 的节点中保存映射关系,以便我们能够在旧 children 的节点中找到可复用的节点。这时候我们就需要给 children 中的节点添加唯一标识,也就是我们常说的 key,在没有 key 的情况下,我们是没办法知道新 children 中的节点是否可以在旧 children 中找到可复用的节点的,如下图所示:
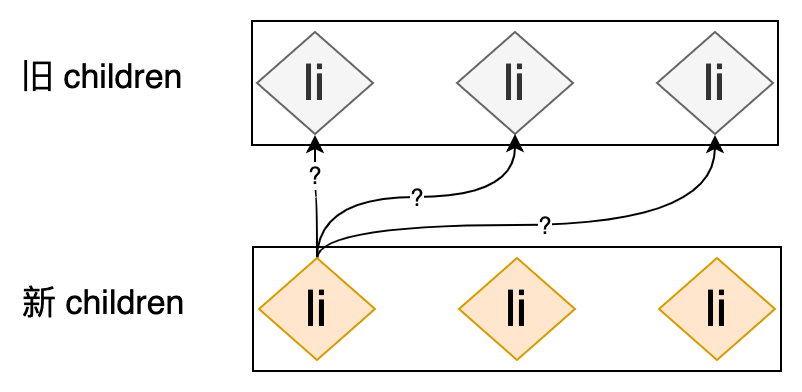
新旧 children 中的节点都是 li 标签,以新 children 的第一个 li 标签为例,你能说出在旧 children 中哪一个 li 标签可被它复用吗?不能,所以,为了明确的知道新旧 children 中节点的映射关系,我们需要在 VNode 创建伊始就为其添加唯一的标识,即 key 属性。
我们可以在使用 h 函数创建 VNode 时,通过 VNodeData 为即将创建的 VNode 设置一个 key:
h('li', { key: 'a' }, 1)
但是为了 diff 算法更加方便的读取一个 VNode 的 key,我们应该在创建 VNode 时将 VNodeData 中的 key 添加到 VNode 本身,所以我们需要修改一下 h 函数,如下:
export function h(tag, data = null, children = null) {
// 省略...
// 返回 VNode 对象
return {
_isVNode: true,
flags,
tag,
data,
key: data && data.key ? data.key : null,
children,
childFlags,
el: null
}
}
如上代码所示,我们在创建 VNode 时,如果 VNodeData 中存在 key 属性,则我们会把其添加到 VNode 对象本身。
现在,在创建 VNode 时已经可以为 VNode 添加唯一标识了,我们使用 key 来修改之前的例子,如下:
// 旧 children
[
h('li', { key: 'a' }, 1),
h('li', { key: 'b' }, 2),
h('li', { key: 'c' }, 3)
]
// 新 children
[
h('li', { key: 'c' }, 3)
h('li', { key: 'a' }, 1),
h('li', { key: 'b' }, 2)
]
有了 key 我们就能够明确的知道新旧 children 中节点的映射关系,如下图所示:
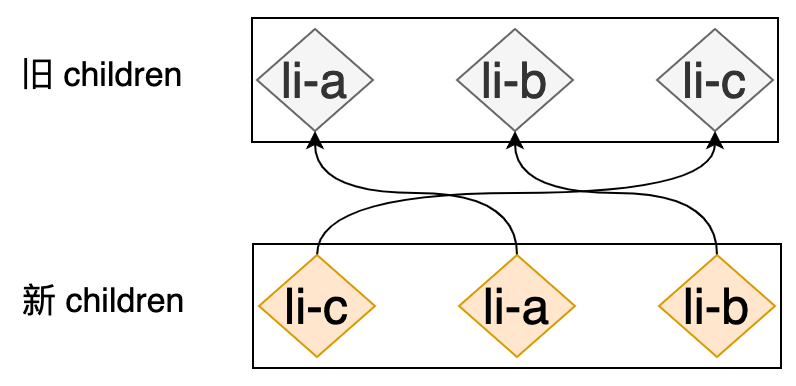
知道了映射关系,我们就很容易判断新 children 中的节点是否可被复用:只需要遍历新 children 中的每一个节点,并去旧 children 中寻找是否存在具有相同 key 值的节点,如下代码所示:
// 遍历新的 children
for (let i = 0; i < nextChildren.length; i++) {
const nextVNode = nextChildren[i]
let j = 0
// 遍历旧的 children
for (j; j < prevChildren.length; j++) {
const prevVNode = prevChildren[j]
// 如果找到了具有相同 key 值的两个节点,则调用 `patch` 函数更新之
if (nextVNode.key === prevVNode.key) {
patch(prevVNode, nextVNode, container)
break // 这里需要 break
}
}
}
这段代码中有两层嵌套的 for 循环语句,外层循环用于遍历新 children,内层循环用于遍历旧 children,其目的是尝试寻找具有相同 key 值的两个节点,如果找到了,则认为新 children 中的节点可以复用旧 children 中已存在的节点,这时我们仍然需要调用 patch 函数对节点进行更新,如果新节点相对于旧节点的 VNodeData 和子节点都没有变化,则 patch 函数什么都不会做(这是优化的关键所在),如果新节点相对于旧节点的 VNodeData 或子节点有变化,则 patch 函数保证了更新的正确性。
# 找到需要移动的节点
现在我们已经找到了可复用的节点,并进行了合适的更新操作,下一步需要做的,就是判断一个节点是否需要移动以及如何移动。如何判断节点是否需要移动呢?为了弄明白这个问题,我们可以先考虑不需要移动的情况,当新旧 children 中的节点顺序不变时,就不需要额外的移动操作,如下:
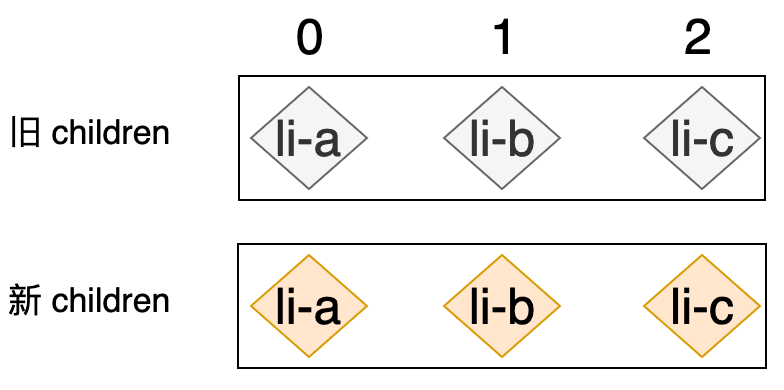
上图中的数字代表着节点在旧 children 中的索引,我们来尝试执行一下本节介绍的算法,看看会发生什么:
- 1、取出新
children的第一个节点,即li-a,并尝试在旧children中寻找li-a,结果是我们找到了,并且li-a在旧children中的索引为0。 - 2、取出新
children的第二个节点,即li-b,并尝试在旧children中寻找li-b,也找到了,并且li-b在旧children中的索引为1。 - 3、取出新
children的第三个节点,即li-c,并尝试在旧children中寻找li-c,同样找到了,并且li-c在旧children中的索引为2。
总结一下我们在“寻找”的过程中,先后遇到的索引顺序为:0->1->2。这是一个递增的顺序,这说明如果在寻找的过程中遇到的索引呈现递增趋势,则说明新旧 children 中节点顺序相同,不需要移动操作。相反的,如果在寻找的过程中遇到的索引值不呈现递增趋势,则说明需要移动操作,举个例子,下图展示了新旧 children 中的节点顺序不一致的情况:
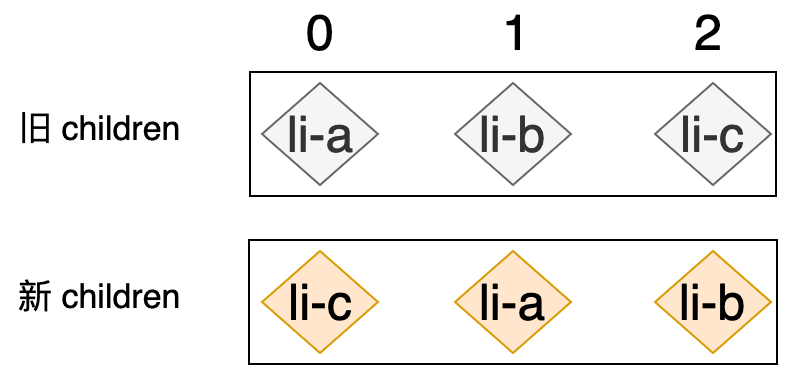
我们同样执行一下本节介绍的算法,看看会发生什么:
- 1、取出新
children的第一个节点,即li-c,并尝试在旧children中寻找li-c,结果是我们找到了,并且li-c在旧children中的索引为2。 - 2、取出新
children的第二个节点,即li-a,并尝试在旧children中寻找li-a,也找到了,并且li-a在旧children中的索引为0。
到了这里,递增的趋势被打破了,我们在寻找的过程中先遇到的索引值是 2,接着又遇到了比 2 小的 0,这说明在旧 children 中 li-a 的位置要比 li-c 靠前,但在新的 children 中 li-a 的位置要比 li-c 靠后。这时我们就知道了 li-a 是那个需要被移动的节点,我们接着往下执行。
- 3、取出新
children的第三个节点,即li-b,并尝试在旧children中寻找li-b,同样找到了,并且li-b在旧children中的索引为1。
我们发现 1 同样小于 2,这说明在旧 children 中节点 li-b 的位置也要比 li-c 的位置靠前,但在新的 children 中 li-b 的位置要比 li-c 靠后。所以 li-b 也需要被移动。
以上我们过程就是我们寻找需要移动的节点的过程,在这个过程中我们发现一个重要的数字:2,是这个数字的存在才使得我们能够知道哪些节点需要移动,我们可以给这个数字一个名字,叫做:寻找过程中在旧 children 中所遇到的最大索引值。如果在后续寻找的过程中发现存在索引值比最大索引值小的节点,意味着该节点需要被移动。
实际上,这就是 React 所使用的算法。我们可以使用一个叫做 lastIndex 的变量存储寻找过程中遇到的最大索引值,并且它的初始值为 0,如下代码所示:
// 用来存储寻找过程中遇到的最大索引值
let lastIndex = 0
// 遍历新的 children
for (let i = 0; i < nextChildren.length; i++) {
const nextVNode = nextChildren[i]
let j = 0
// 遍历旧的 children
for (j; j < prevChildren.length; j++) {
const prevVNode = prevChildren[j]
// 如果找到了具有相同 key 值的两个节点,则调用 `patch` 函数更新之
if (nextVNode.key === prevVNode.key) {
patch(prevVNode, nextVNode, container)
if (j < lastIndex) {
// 需要移动
} else {
// 更新 lastIndex
lastIndex = j
}
break // 这里需要 break
}
}
}
如上代码中,变量 j 是节点在旧 children 中的索引,如果它小于 lastIndex 则代表当前遍历到的节点需要移动,否则我们就使用 j 的值更新 lastIndex 变量的值,这就保证了 lastIndex 所存储的总是我们在旧 children 中所遇到的最大索引。
# 移动节点
现在我们已经有办法找到需要移动的节点了,接下来要解决的问题就是:应该如何移动这些节点?为了弄明白这个问题,我们还是先来看下图:

新 children 中的第一个节点是 li-c,它在旧 children 中的索引为 2,由于 li-c 是新 children 中的第一个节点,所以它始终都是不需要移动的,只需要调用 patch 函数更新即可,如下图:
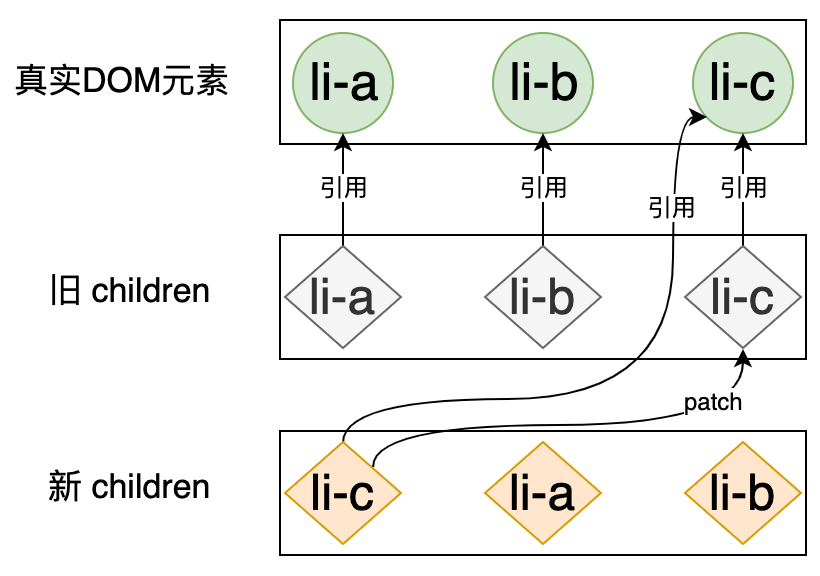
这里我们需要注意的,也是非常重要的一点是:新 children 中的 li-c 节点在经过 patch 函数之后,也将存在对真实 DOM 元素的引用。下面的代码可以证明这一点:
function patchElement(prevVNode, nextVNode, container) {
// 省略...
// 拿到 el 元素,注意这时要让 nextVNode.el 也引用该元素
const el = (nextVNode.el = prevVNode.el)
// 省略...
}
beforeCreate() {
this.$options.data = {...}
}
如上代码所示,这是 patchElement 函数中的一段代码,在更新新旧 VNode 时,新的 VNode 通过旧 VNode 的 el 属性实现了对真实 DOM 的引用。为什么说这一点很关键呢?继续往下看。
li-c 节点更新完毕,接下来是新 children 中的第二个节点 li-a,它在旧 children 中的索引是 0,由于 0 < 2 所以 li-a 是需要移动的节点,那应该怎么移动呢?很简单,新 children 中的节点顺序实际上就是更新完成之后,节点应有的最终顺序,通过观察新 children 可知,新 children 中 li-a 节点的前一个节点是 li-c,所以我们的移动方案应该是:把 li-a 节点对应的真实 DOM 移动到 li-c 节点所对应真实 DOM 的后面。这里的关键在于移动的是真实 DOM 而非 VNode。所以我们需要分别拿到 li-c 和 li-a 所对应的真实 DOM,这时就体现出了上面提到的关键点:新 children 中的 li-c 已经存在对真实 DOM 的引用了,所以我们很容易就能拿到 li-c 对应的真实 DOM。对于获取 li-a 节点所对应的真实 DOM 将更加容易,由于我们当前遍历到的节点就是 li-a,所以我们可以直接通过旧 children 中的 li-a 节点拿到其真实 DOM 的引用,如下代码所示:
// 用来存储寻找过程中遇到的最大索引值
let lastIndex = 0
// 遍历新的 children
for (let i = 0; i < nextChildren.length; i++) {
const nextVNode = nextChildren[i]
let j = 0
// 遍历旧的 children
for (j; j < prevChildren.length; j++) {
const prevVNode = prevChildren[j]
// 如果找到了具有相同 key 值的两个节点,则调用 `patch` 函数更新之
if (nextVNode.key === prevVNode.key) {
patch(prevVNode, nextVNode, container)
if (j < lastIndex) {
// 需要移动
// refNode 是为了下面调用 insertBefore 函数准备的
const refNode = nextChildren[i - 1].el.nextSibling
// 调用 insertBefore 函数移动 DOM
container.insertBefore(prevVNode.el, refNode)
} else {
// 更新 lastIndex
lastIndex = j
}
break // 这里需要 break
}
}
}
观察如上代码段中高亮的部分,实际上这两句代码即可完成 DOM 的移动操作。我们来对这两句代码的工作方式做一个详细的解释,假设我们当前正在更新的节点是 li-a,那么如上代码中的变量 i 就是节点 li-a 在新 children 中的位置索引。所以 nextChildren[i - 1] 就是 li-a 节点的前一个节点,也就是 li-c 节点,由于 li-c 节点存在对真实 DOM 的引用,所以我们可以通过其 el 属性拿到真实 DOM,到了这一步,li-c 节点的所对应的真实 DOM 我们已经得到了。但不要忘记我们的目标是:把 li-a 节点对应的真实 DOM 移动到 li-c 节点所对应真实 DOM 的后面,所以我们的思路应该是想办法拿到 li-c 节点对应真实 DOM 的下一个兄弟节点,并把 li-a 节点所对应真实 DOM 插到该节点的前面,这才能保证移动的正确性。所以上面的代码中常量 refNode 引用是 li-c 节点对应真实 DOM 的下一个兄弟节点。拿到了正确的 refNode 之后,我们就可以调用容器元素的 insertBefore 方法来完成 DOM 的移动了,移动的对象就是 li-a 节点所对应的真实 DOM,由于当前正在处理的就是 li-a 节点,所以 prevVNode 就是旧 children 中的 li-a 节点,它是存在对真实 DOM 的引用的,即 prevVNode.el。万事俱备,移动工作将顺利完成。说起来有些抽象,用一张图可以更加清晰的描述这个过程:
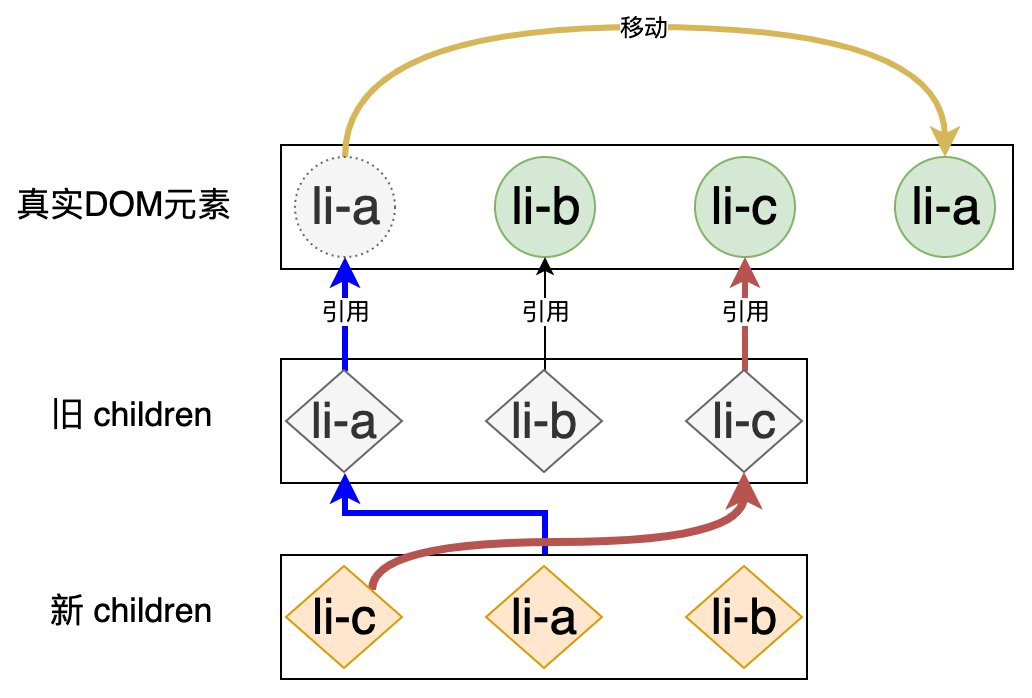
观察不同颜色的线条,关键在于我们要找到 VNode 所引用的真实 DOM,然后把真实 DOM 按照新 children 中节点间的关系进行移动,由于新 children 中节点的顺序就是最终的目标顺序,所以移动之后的真实 DOM 的顺序也会是最终的目标顺序。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/4x6qo5w34w (opens new window)
# 添加新元素
在上面的讲解中,我们一直忽略了一个问题,即新 children 中可能包含那些不能够通过移动来完成更新的节点,例如新 children 中包含了一个全新的节点,这意味着在旧 children 中是找不到该节点的,如下图所示:
节点 li-d 在旧的 children 中是不存在的,所以当我们尝试在旧的 children 中寻找 li-d 节点时,是找不到可复用节点的,这时就没办法通过移动节点来完成更新操作,所以我们应该使用 mount 函数将 li-d 节点作为全新的 VNode 挂载到合适的位置。
我们将面临两个问题,第一个问题是:如何知道一个节点在旧的 children 中是不存在的?这个问题比较好解决,如下代码所示:
let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {
const nextVNode = nextChildren[i]
let j = 0,
find = false
for (j; j < prevChildren.length; j++) {
const prevVNode = prevChildren[j]
if (nextVNode.key === prevVNode.key) {
find = true
patch(prevVNode, nextVNode, container)
if (j < lastIndex) {
// 需要移动
const refNode = nextChildren[i - 1].el.nextSibling
container.insertBefore(prevVNode.el, refNode)
break
} else {
// 更新 lastIndex
lastIndex = j
}
}
}
}
如上高亮代码所示,我们在原来的基础上添加了变量 find,它将作为一个标志,代表新 children 中的节点是否存在于旧 children 中,初始值为 false,一旦在旧 children 中寻找到了相应的节点,我们就将变量 find 的值设置为 true,所以如果内层循环结束后,变量 find 的值仍然为 false,则说明在旧的 children 中找不到可复用的节点,这时我们就需要使用 mount 函数将当前遍历到的节点挂载到容器元素,如下高亮的代码所示:
let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {
const nextVNode = nextChildren[i]
let j = 0,
find = false
for (j; j < prevChildren.length; j++) {
const prevVNode = prevChildren[j]
if (nextVNode.key === prevVNode.key) {
find = true
patch(prevVNode, nextVNode, container)
if (j < lastIndex) {
// 需要移动
const refNode = nextChildren[i - 1].el.nextSibling
container.insertBefore(prevVNode.el, refNode)
break
} else {
// 更新 lastIndex
lastIndex = j
}
}
}
if (!find) {
// 挂载新节点
mount(nextVNode, container, false)
}
}
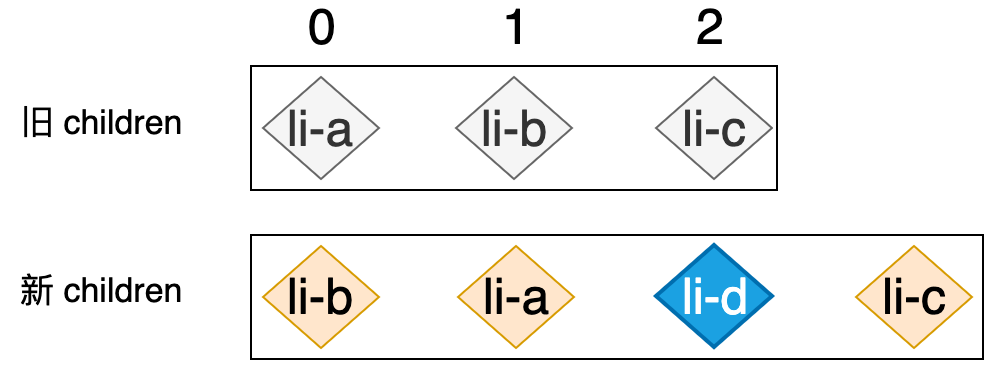
当内层循环结束之后,如果变量 find 的值仍然为 false,则说明 nextVNode 是全新的节点,所以我们直接调用 mount 函数将其挂载到容器元素 container 中。但是很遗憾,这段代码不能正常的工作,这是因为我们之前编写的 mountElement 函数存在缺陷,它总是调用 appendChild 方法插入 DOM 元素,所以上面的代码始终会把新的节点作为容器元素的最后一个子节点添加到末尾,这不是我们想要的结果,我们应该按照节点在新的 children 中的位置将其添加到正确的地方,如下图所示:

新的 li-d 节点紧跟在 li-a 节点的后面,所以正确的做法应该是把 li-d 节点添加到 li-a 节点所对应真实 DOM 的后面才行。如何才能保证 li-d 节点始终被添加到 li-a 节点的后面呢?答案是使用 insertBefore 方法代替 appendChild 方法,我们可以找到 li-a 节点所对应真实 DOM 的下一个节点,然后将 li-d 节点插入到该节点之前即可,如下高亮代码所示:
let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {
const nextVNode = nextChildren[i]
let j = 0,
find = false
for (j; j < prevChildren.length; j++) {
const prevVNode = prevChildren[j]
if (nextVNode.key === prevVNode.key) {
find = true
patch(prevVNode, nextVNode, container)
if (j < lastIndex) {
// 需要移动
const refNode = nextChildren[i - 1].el.nextSibling
container.insertBefore(prevVNode.el, refNode)
break
} else {
// 更新 lastIndex
lastIndex = j
}
}
}
if (!find) {
// 挂载新节点
// 找到 refNode
const refNode =
i - 1 < 0
? prevChildren[0].el
: nextChildren[i - 1].el.nextSibling
mount(nextVNode, container, false, refNode)
}
}
我们先找到当前遍历到的节点的前一个节点,即 nextChildren[i - 1],接着找到该节点所对应真实 DOM 的下一个子节点作为 refNode,即 nextChildren[i - 1].el.nextSibling,但是由于当前遍历到的节点有可能是新 children 的第一个节点,这时 i - 1 < 0,这将导致 nextChildren[i - 1] 不存在,所以当 i - 1 < 0 时,我们就知道新的节点是作为第一个节点而存在的,这时我们只需要把新的节点插入到最前面即可,所以我们使用 prevChildren[0].el 作为 refNode。最后调用 mount 函数挂载新节点时,我们为其传递了第四个参数 refNode,当 refNode 存在时,我们应该使用 insertBefore 方法代替 appendChild 方法,这就需要我们修改之前实现的 mount 函数了 mountElement 函数,为它们添加第四个参数,如下:
// mount 函数
function mount(vnode, container, isSVG, refNode) {
const { flags } = vnode
if (flags & VNodeFlags.ELEMENT) {
// 挂载普通标签
mountElement(vnode, container, isSVG, refNode)
}
// 省略...
}
// mountElement 函数
function mountElement(vnode, container, isSVG, refNode) {
// 省略...
refNode ? container.insertBefore(el, refNode) : container.appendChild(el)
}
这样,当新 children 中存在全新的节点时,我们就能够保证正确的将其添加到容器元素内了。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/54215km3vn (opens new window)
TIP
实际上,所有与挂载和 patch 相关的函数都应该接收 refNode 作为参数,这里我们旨在让读者掌握核心思路,避免讲解过程的冗杂。
# 移除不存在的元素
除了要将全新的节点添加到容器元素之外,我们还应该把已经不存在了的节点移除,如下图所示:
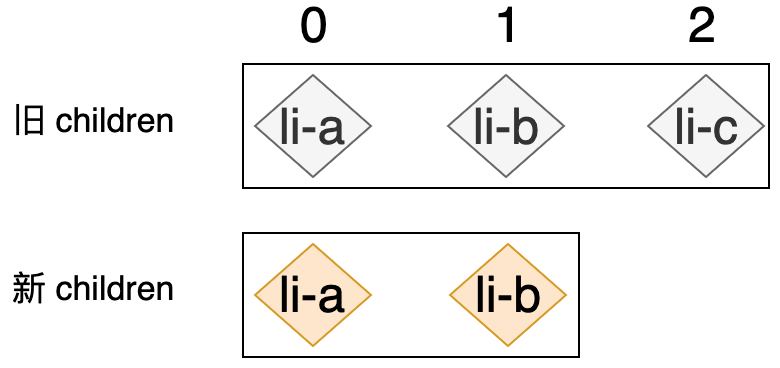
可以看出,新的 children 中已经不存在 li-c 节点了,所以我们应该想办法将 li-c 节点对应的真实 DOM 从容器元素内移除。但我们之前编写的算法还不能完成这个任务,因为外层循环遍历的是新的 children,所以外层循环会执行两次,第一次用于处理 li-a 节点,第二次用于处理 li-b 节点,此时整个算法已经运行结束了。所以,我们需要在外层循环结束之后,再优先遍历一次旧的 children,并尝试拿着旧 children 中的节点去新 children 中寻找相同的节点,如果找不到则说明该节点已经不存在于新 children 中了,这时我们应该将该节点对应的真实 DOM 移除,如下高亮代码所示:
let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {
const nextVNode = nextChildren[i]
let j = 0,
find = false
for (j; j < prevChildren.length; j++) {
// 省略...
}
if (!find) {
// 挂载新节点
// 省略...
}
}
// 移除已经不存在的节点
// 遍历旧的节点
for (let i = 0; i < prevChildren.length; i++) {
const prevVNode = prevChildren[i]
// 拿着旧 VNode 去新 children 中寻找相同的节点
const has = nextChildren.find(
nextVNode => nextVNode.key === prevVNode.key
)
if (!has) {
// 如果没有找到相同的节点,则移除
container.removeChild(prevVNode.el)
}
}
TIP
完整代码&在线体验地址:https://codesandbox.io/s/844lp3mq72 (opens new window)
至此,第一个完整的 Diff 算法我们就讲解完毕了,这个算法就是 React 所采用的 Diff 算法。但该算法仍然存在可优化的空间,我们将在下一小节继续讨论。
# 另一个思路 - 双端比较
# 双端比较的原理
刚刚提到了 React 的 Diff 算法是存在优化空间的,想要要找到优化的关键点,我们首先要知道它存在什么问题。来看下图:
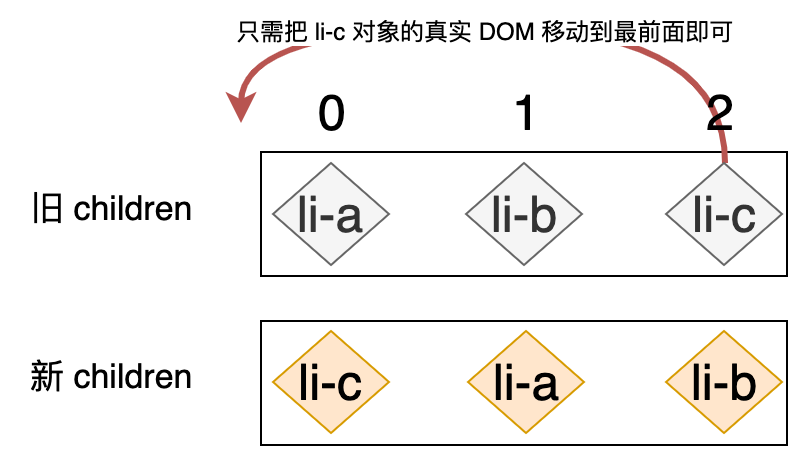
在这个例子中,我们可以通过肉眼观察从而得知最优的解决方案应该是:把 li-c 节点对应的真实 DOM 移动到最前面即可,只需要一次移动即可完成更新。然而,React 所采用的 Diff 算法在更新如上案例的时候,会进行两次移动:
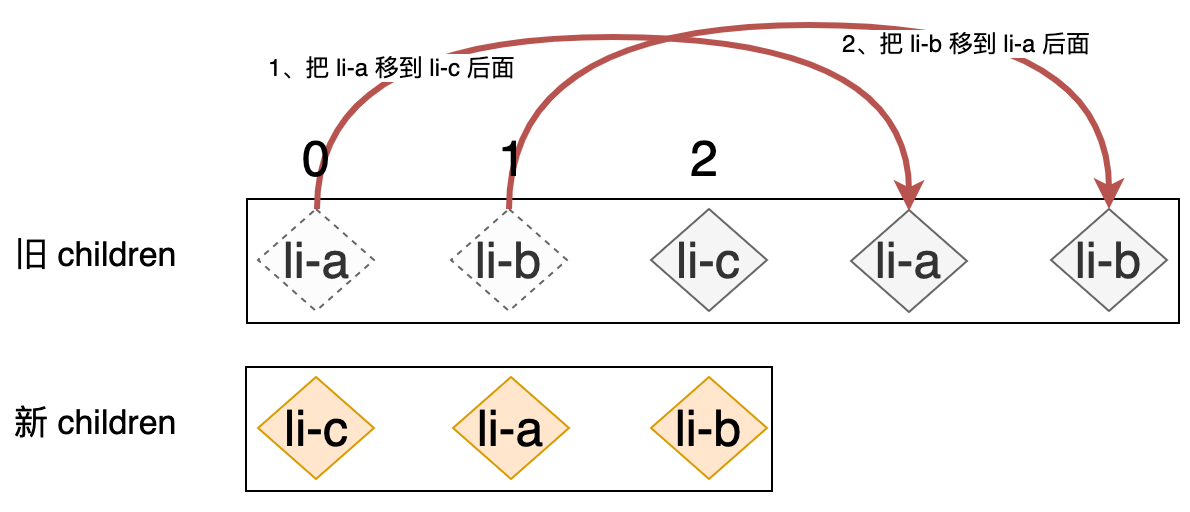
显然,这种做法必然会造成额外的性能开销。那么有没有办法来避免这种多余的 DOM 移动呢?当然有办法,那就是我们接下来要介绍的一个新的思路:双端比较。
所谓双端比较,就是同时从新旧 children 的两端开始进行比较的一种方式,所以我们需要四个索引值,分别指向新旧 children 的两端,如下图所示:
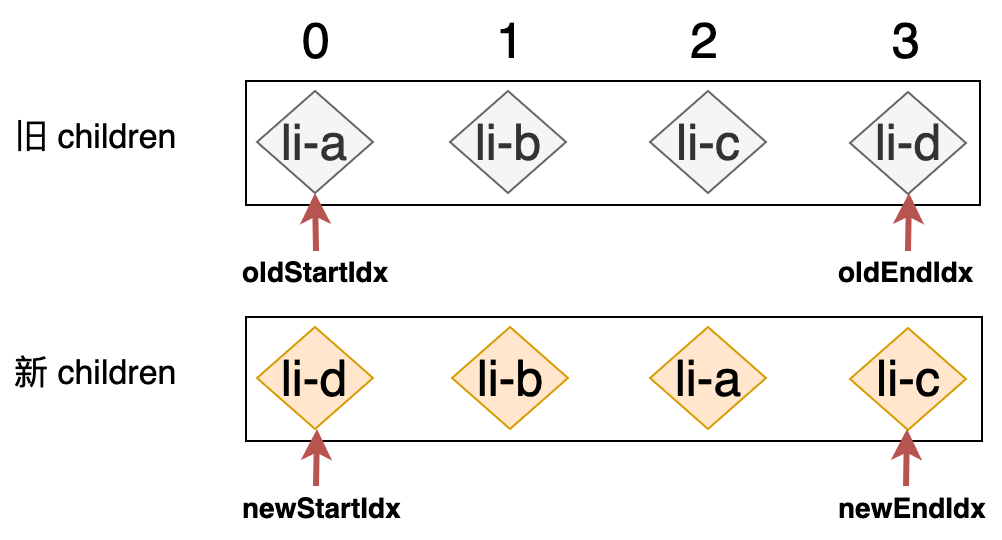
我们使用四个变量 oldStartIdx、oldEndIdx、newStartIdx 以及 newEndIdx 分别存储旧 children 和新 children 的两个端点的位置索引,可以用如下代码来表示:
let oldStartIdx = 0
let oldEndIdx = prevChildren.length - 1
let newStartIdx = 0
let newEndIdx = nextChildren.length - 1
除了位置索引之外,我们还需要拿到四个位置索引所指向的 VNode:
let oldStartVNode = prevChildren[oldStartIdx]
let oldEndVNode = prevChildren[oldEndIdx]
let newStartVNode = nextChildren[newStartIdx]
let newEndVNode = nextChildren[newEndIdx]
有了这些基础信息,我们就可以开始执行双端比较了,在一次比较过程中,最多需要进行四次比较:
- 1、使用旧
children的头一个VNode与新children的头一个VNode比对,即oldStartVNode和newStartVNode比较对。 - 2、使用旧
children的最后一个VNode与新children的最后一个VNode比对,即oldEndVNode和newEndVNode比对。 - 3、使用旧
children的头一个VNode与新children的最后一个VNode比对,即oldStartVNode和newEndVNode比对。 - 4、使用旧
children的最后一个VNode与新children的头一个VNode比对,即oldEndVNode和newStartVNode比对。
在如上四步比对过程中,试图去寻找可复用的节点,即拥有相同 key 值的节点。这四步比对中,在任何一步中寻找到了可复用节点,则会停止后续的步骤,可以用下图来描述在一次比对过程中的四个步骤:
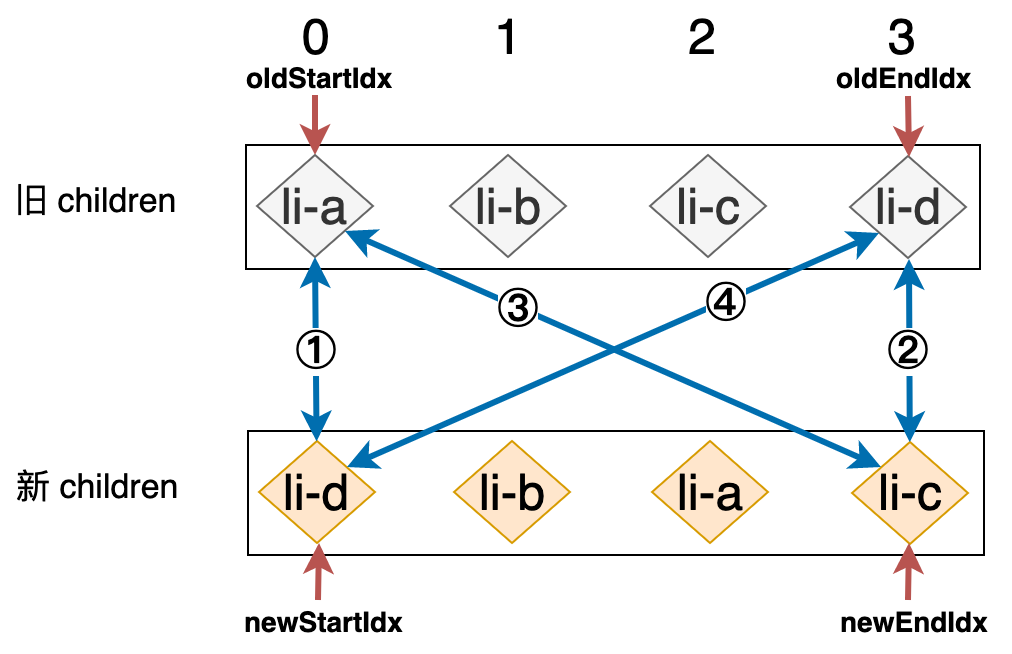
如下代码是该比对过程的实现:
if (oldStartVNode.key === newStartVNode.key) {
// 步骤一:oldStartVNode 和 newStartVNode 比对
} else if (oldEndVNode.key === newEndVNode.key) {
// 步骤二:oldEndVNode 和 newEndVNode 比对
} else if (oldStartVNode.key === newEndVNode.key) {
// 步骤三:oldStartVNode 和 newEndVNode 比对
} else if (oldEndVNode.key === newStartVNode.key) {
// 步骤四:oldEndVNode 和 newStartVNode 比对
}
每次比对完成之后,如果在某一步骤中找到了可复用的节点,我们就需要将相应的位置索引后移/前移一位。以上图为例:
- 第一步:拿旧
children中的li-a和新children中的li-d进行比对,由于二者key值不同,所以不可复用,什么都不做。 - 第二步:拿旧
children中的li-d和新children中的li-c进行比对,同样不可复用,什么都不做。 - 第三步:拿旧
children中的li-a和新children中的li-c进行比对,什么都不做。 - 第四部:拿旧
children中的li-d和新children中的li-d进行比对,由于这两个节点拥有相同的key值,所以我们在这次比对的过程中找到了可复用的节点。
由于我们在第四步的比对中找到了可复用的节点,即 oldEndVNode 和 newStartVNode 拥有相同的 key 值,这说明:li-d 节点所对应的真实 DOM 原本是最后一个子节点,并且更新之后它应该变成第一个子节点。所以我们需要把 li-d 所对应的真实 DOM 移动到最前方即可:
if (oldStartVNode.key === newStartVNode.key) {
// 步骤一:oldStartVNode 和 newStartVNode 比对
} else if (oldEndVNode.key === newEndVNode.key) {
// 步骤二:oldEndVNode 和 newEndVNode 比对
} else if (oldStartVNode.key === newEndVNode.key) {
// 步骤三:oldStartVNode 和 newEndVNode 比对
} else if (oldEndVNode.key === newStartVNode.key) {
// 步骤四:oldEndVNode 和 newStartVNode 比对
// 先调用 patch 函数完成更新
patch(oldEndVNode, newStartVNode, container)
// 更新完成后,将容器中最后一个子节点移动到最前面,使其成为第一个子节点
container.insertBefore(oldEndVNode.el, oldStartVNode.el)
// 更新索引,指向下一个位置
oldEndVNode = prevChildren[--oldEndIdx]
newStartVNode = nextChildren[++newStartIdx]
}
这一步更新完成之后,新的索引关系可以用下图来表示:
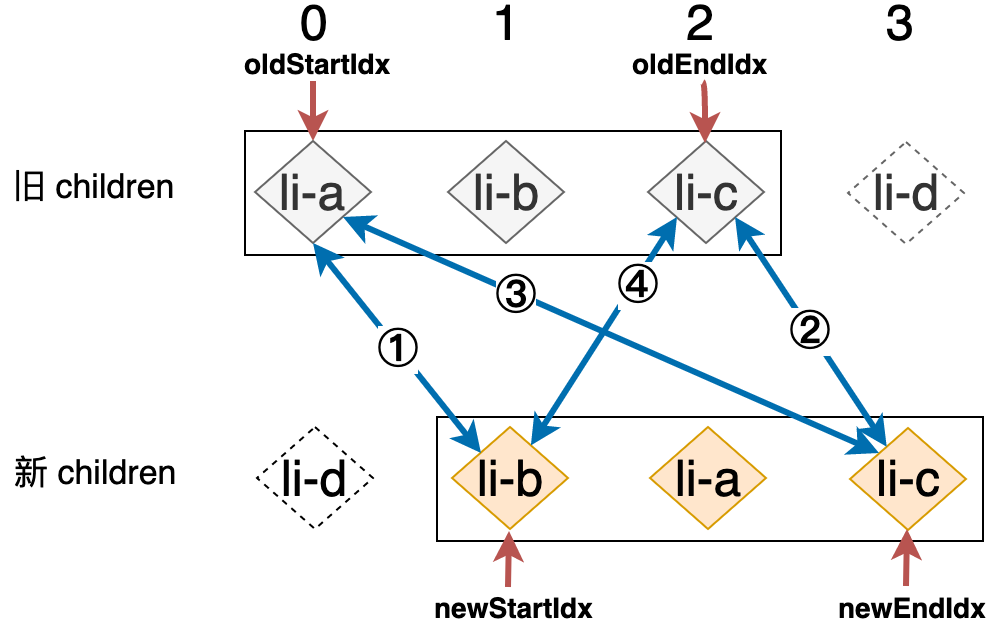
由于 li-d 节点所对应的真实 DOM 元素已经更新完成且被移动,所以现在真实 DOM 的顺序是:li-d、li-a、li-b、li-c,如下图所示:
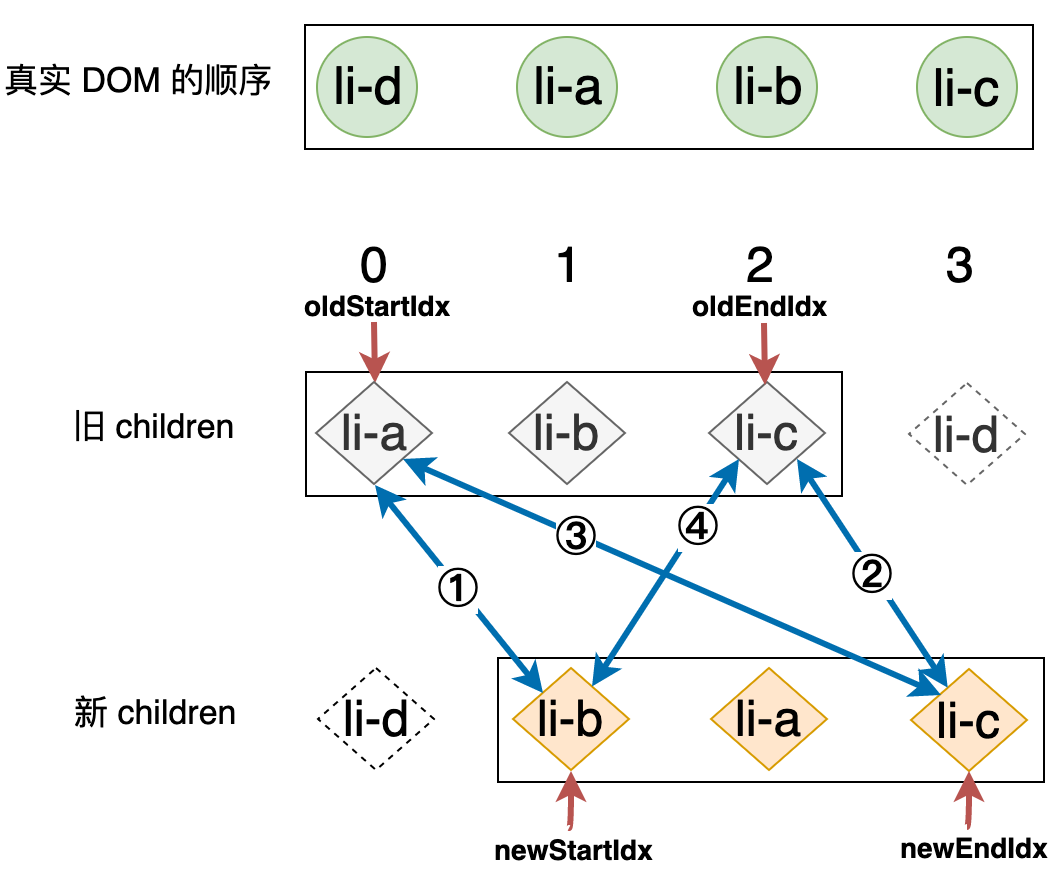
这样,一次比对就完成了,并且位置索引已经更新,我们需要进行下轮的比对,那么什么时候比对才能结束呢?如下代码所示:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (oldStartVNode.key === newStartVNode.key) {
// 步骤一:oldStartVNode 和 newStartVNode 比对
} else if (oldEndVNode.key === newEndVNode.key) {
// 步骤二:oldEndVNode 和 newEndVNode 比对
} else if (oldStartVNode.key === newEndVNode.key) {
// 步骤三:oldStartVNode 和 newEndVNode 比对
} else if (oldEndVNode.key === newStartVNode.key) {
// 步骤四:oldEndVNode 和 newStartVNode 比对
}
}
我们将每一轮比对所做的工作封装到一个 while 循环内,循环结束的条件是要么 oldStartIdx 大于 oldEndIdx,要么 newStartIdx 大于 newEndIdx。
还是观察上图,我们继续进行第二轮的比对:
- 第一步:拿旧
children中的li-a和新children中的li-b进行比对,由于二者key值不同,所以不可复用,什么都不做。 - 第二步:拿旧
children中的li-c和新children中的li-c进行比对,此时,由于二者拥有相同的key,所以是可复用的节点,但是由于二者在新旧children中都是最末尾的一个节点,所以是不需要进行移动操作的,只需要调用patch函数更新即可,同时将相应的索引前移一位,如下高亮代码所示:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (oldStartVNode.key === newStartVNode.key) {
// 步骤一:oldStartVNode 和 newStartVNode 比对
} else if (oldEndVNode.key === newEndVNode.key) {
// 步骤二:oldEndVNode 和 newEndVNode 比对
// 调用 patch 函数更新
patch(oldEndVNode, newEndVNode, container)
// 更新索引,指向下一个位置
oldEndVNode = prevChildren[--oldEndIdx]
newEndVNode = nextChildren[--newEndIdx]
} else if (oldStartVNode.key === newEndVNode.key) {
// 步骤三:oldStartVNode 和 newEndVNode 比对
} else if (oldEndVNode.key === newStartVNode.key) {
// 步骤四:oldEndVNode 和 newStartVNode 比对
// 先调用 patch 函数完成更新
patch(oldEndVNode, newStartVNode, container)
// 更新完成后,将容器中最后一个子节点移动到最前面,使其成为第一个子节点
container.insertBefore(oldEndVNode.el, oldStartVNode.el)
// 更新索引,指向下一个位置
oldEndVNode = prevChildren[--oldEndIdx]
newStartVNode = nextChildren[++newStartIdx]
}
}
由于没有进行移动操作,所以在这一轮比对中,真实 DOM 的顺序没有发生变化,下图表示了在这一轮比对结束之后的状况:
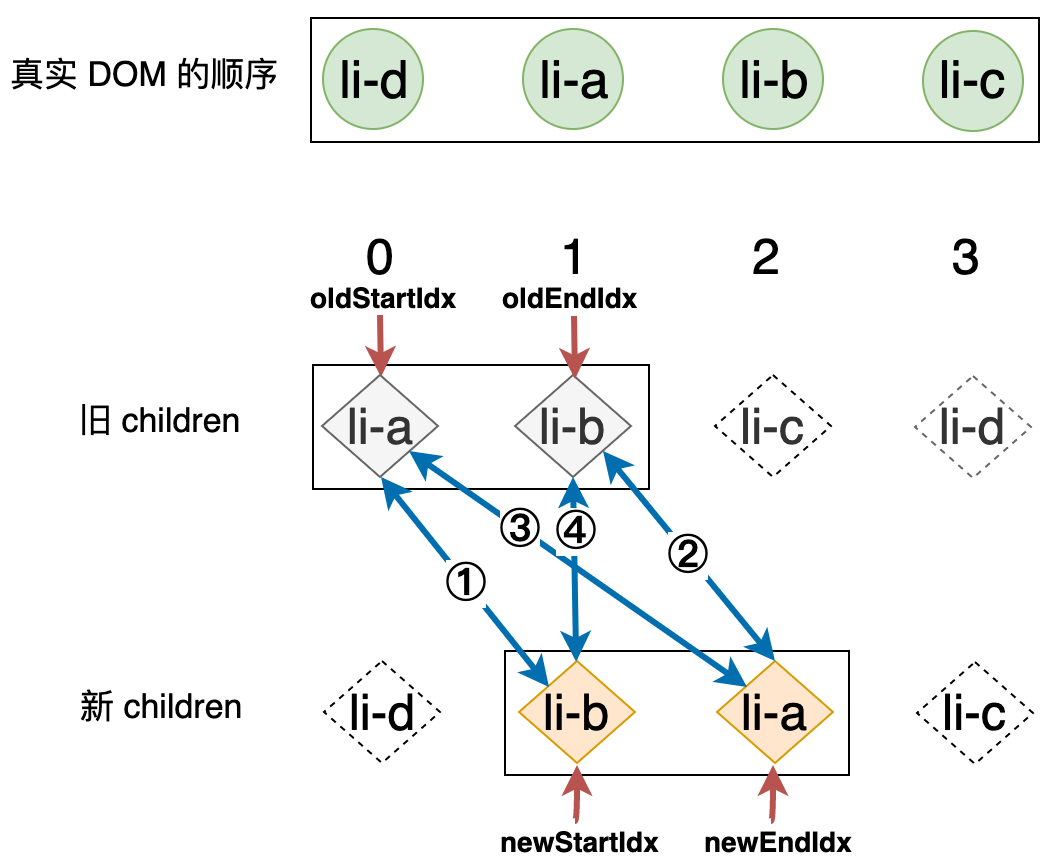
由于此时循环条件成立,所以会继续下一轮的比较:
- 第一步:拿旧
children中的li-a和新children中的li-b进行比对,由于二者key值不同,所以不可复用,什么都不做。 - 第二步:拿旧
children中的li-b和新children中的li-a进行比对,不可复用,什么都不做。 - 第三步:拿旧
children中的li-a和新children中的li-a进行比对,此时,我们找到了可复用的节点。
这一次满足的条件是:oldStartVNode.key === newEndVNode.key,这说明:li-a 节点所对应的真实 DOM 原本是第一个子节点,但现在变成了“最后”一个子节点,这里的“最后”一词使用了引号,这是因为大家要明白“最后”的真正含义,它并不是指真正意义上的最后一个节点,而是指当前索引范围内的最后一个节点。所以移动操作也是比较明显的,我们将 oldStartVNode 对应的真实 DOM 移动到 oldEndVNode 所对应真实 DOM 的后面即可,如下高亮代码所示:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (oldStartVNode.key === newStartVNode.key) {
// 步骤一:oldStartVNode 和 newStartVNode 比对
} else if (oldEndVNode.key === newEndVNode.key) {
// 步骤二:oldEndVNode 和 newEndVNode 比对
// 调用 patch 函数更新
patch(oldEndVNode, newEndVNode, container)
// 更新索引,指向下一个位置
oldEndVNode = prevChildren[--oldEndIdx]
newEndVNode = newEndVNode[--newEndIdx]
} else if (oldStartVNode.key === newEndVNode.key) {
// 步骤三:oldStartVNode 和 newEndVNode 比对
// 调用 patch 函数更新
patch(oldStartVNode, newEndVNode, container)
// 将 oldStartVNode.el 移动到 oldEndVNode.el 的后面,也就是 oldEndVNode.el.nextSibling 的前面
container.insertBefore(
oldStartVNode.el,
oldEndVNode.el.nextSibling
)
// 更新索引,指向下一个位置
oldStartVNode = prevChildren[++oldStartIdx]
newEndVNode = nextChildren[--newEndIdx]
} else if (oldEndVNode.key === newStartVNode.key) {
// 步骤四:oldEndVNode 和 newStartVNode 比对
// 先调用 patch 函数完成更新
patch(oldEndVNode, newStartVNode, container)
// 更新完成后,将容器中最后一个子节点移动到最前面,使其成为第一个子节点
container.insertBefore(oldEndVNode.el, oldStartVNode.el)
// 更新索引,指向下一个位置
oldEndVNode = prevChildren[--oldEndIdx]
newStartVNode = nextChildren[++newStartIdx]
}
}
在这一步的更新中,真实 DOM 的顺序是有变化的,li-a 节点对应的真实 DOM 被移到了 li-b 节点对应真实 DOM 的后面,同时由于位置索引也在相应的移动,所以在这一轮更新之后,现在的结果看上去应该如下图所示:
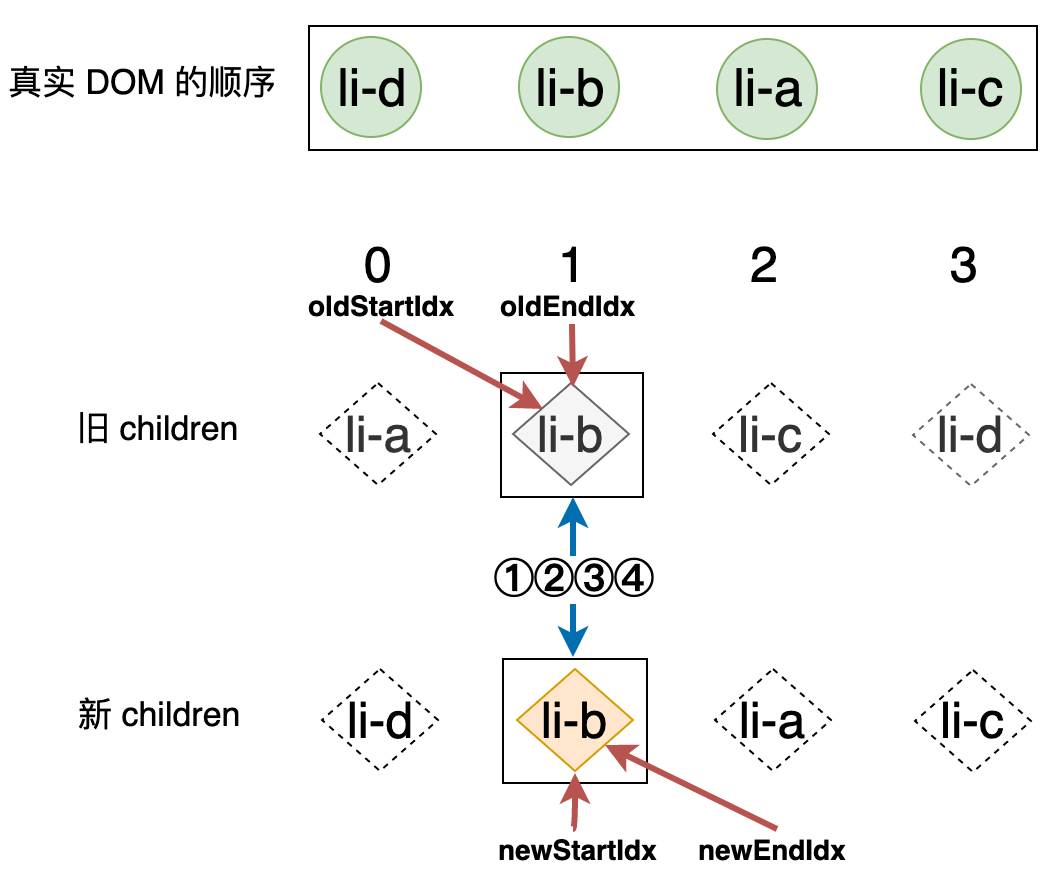
现在 oldStartIdx 和 oldEndIdx 指向了同一个位置,即旧 children 中的 li-b 节点。同样的 newStartIdx 和 newEndIdx 也指向了同样的位置,即新 children 中的 li-b。由于此时仍然满足循环条件,所以会继续下一轮的比对:
- 第一步:拿旧
children中的li-b和新children中的li-b进行比对,二者拥有相同的key,可复用。
此时,在第一步的时候就已经找到了可复用的节点,满足的条件是:oldStartVNode.key === newStartVNode.key,但是由于该节点无论是在新 children 中还是旧 children 中,都是“第一个”节点,所以位置不需要变化,即不需要移动操作,只需要调用 patch 函数更新即可,同时也要将相应的位置所以下移一位,如下高亮代码所示:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (oldStartVNode.key === newStartVNode.key) {
// 步骤一:oldStartVNode 和 newStartVNode 比对
// 调用 patch 函数更新
patch(oldStartVNode, newStartVNode, container)
// 更新索引,指向下一个位置
oldStartVNode = prevChildren[++oldStartIdx]
newStartVNode = nextChildren[++newStartIdx]
} else if (oldEndVNode.key === newEndVNode.key) {
// 省略...
} else if (oldStartVNode.key === newEndVNode.key) {
// 省略...
} else if (oldEndVNode.key === newStartVNode.key) {
// 省略...
}
}
在这一轮更新完成之后,虽然没有进行任何移动操作,但是我们发现,真实 DOM 的顺序,已经与新 children 中节点的顺序保持一致了,也就是说我们圆满的完成了目标,如下图所示:
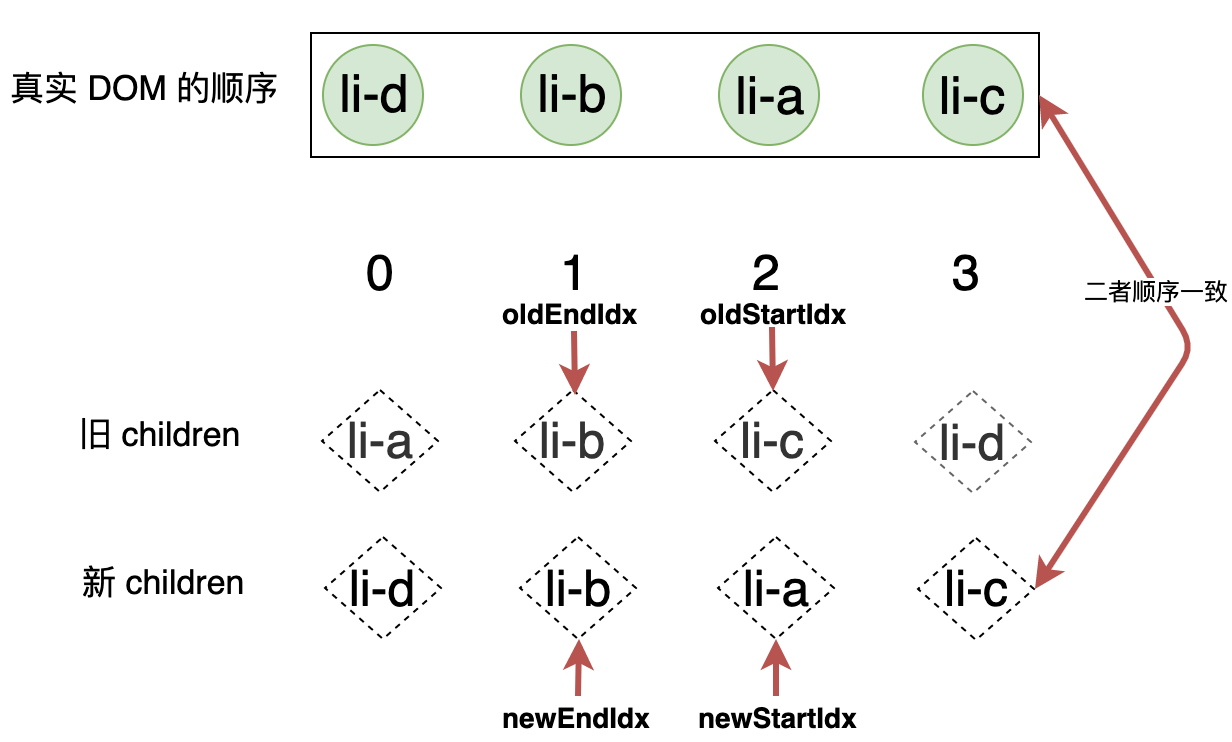
另外,观察上图可以发现,此时 oldStartIdx 和 newStartIdx 分别比 oldEndIdx 和 newEndIdx 要大,所以这将是最后一轮的比对,循环将终止,以上就是双端比较的核心原理。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/xvmqn58jqw (opens new window)
# 双端比较的优势
理解了双端比较的原理之后,我们来看一下双端比较所带来的优势,还是拿之前的例子,如下:

前面分析过,如果采用 React 的方式来对上例进行更新,则会执行两次移动操作,首先会把 li-a 节点对应的真实 DOM 移动到 li-c 节点对应的真实 DOM 的后面,接着再把 li-b 节点所对应的真实 DOM 移动到 li-a 节点所对应真实 DOM 的后面,即:

接下来我们采用双端比较的方式,来完成上例的更新,看看会有什么不同,如下图所示:
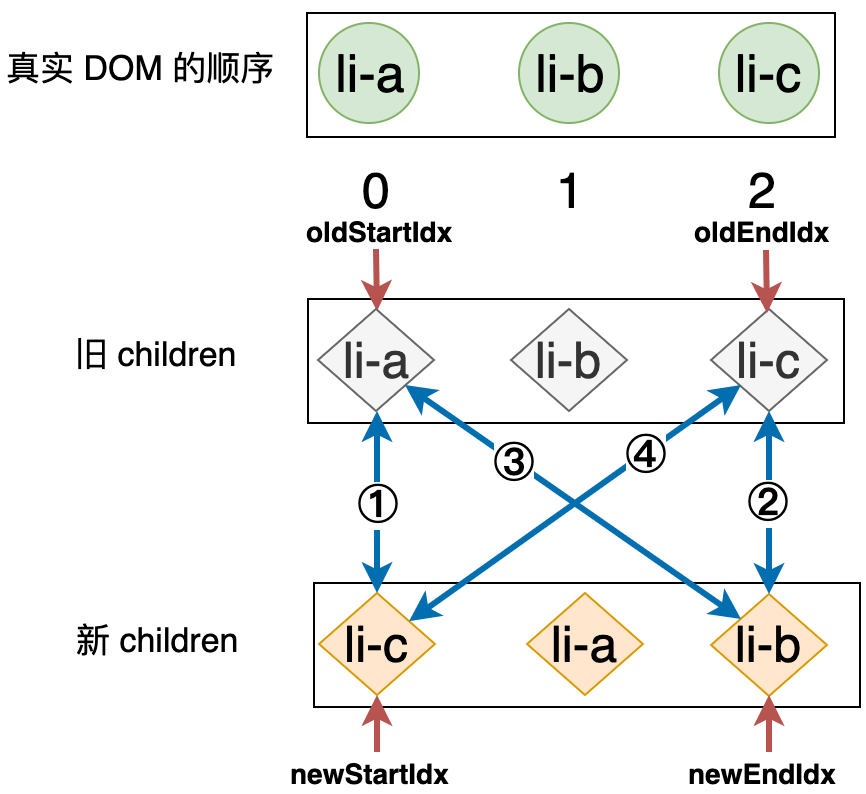
我们按照双端比较的思路开始第一轮比较,按步骤执行:
- 第一步:拿旧
children中的li-a和新children中的li-c进行比对,由于二者key值不同,所以不可复用,什么都不做。 - 第二步:拿旧
children中的li-c和新children中的li-b进行比对,不可复用,什么都不做。 - 第三步:拿旧
children中的li-a和新children中的li-b进行比对,不可复用,什么都不做。 - 第四步:拿旧
children中的li-c和新children中的li-c进行比对,此时,两个节点拥有相同的key值,可复用。
到了第四步,对于 li-c 节点来说,它原本是整个 children 的最后一个子节点,但是现在变成了新 children 的第一个子节点,按照上端比较的算法逻辑,此时会把 li-c 节点所对应的真实 DOM 移动到 li-a 节点所对应真实 DOM 的前面,即:
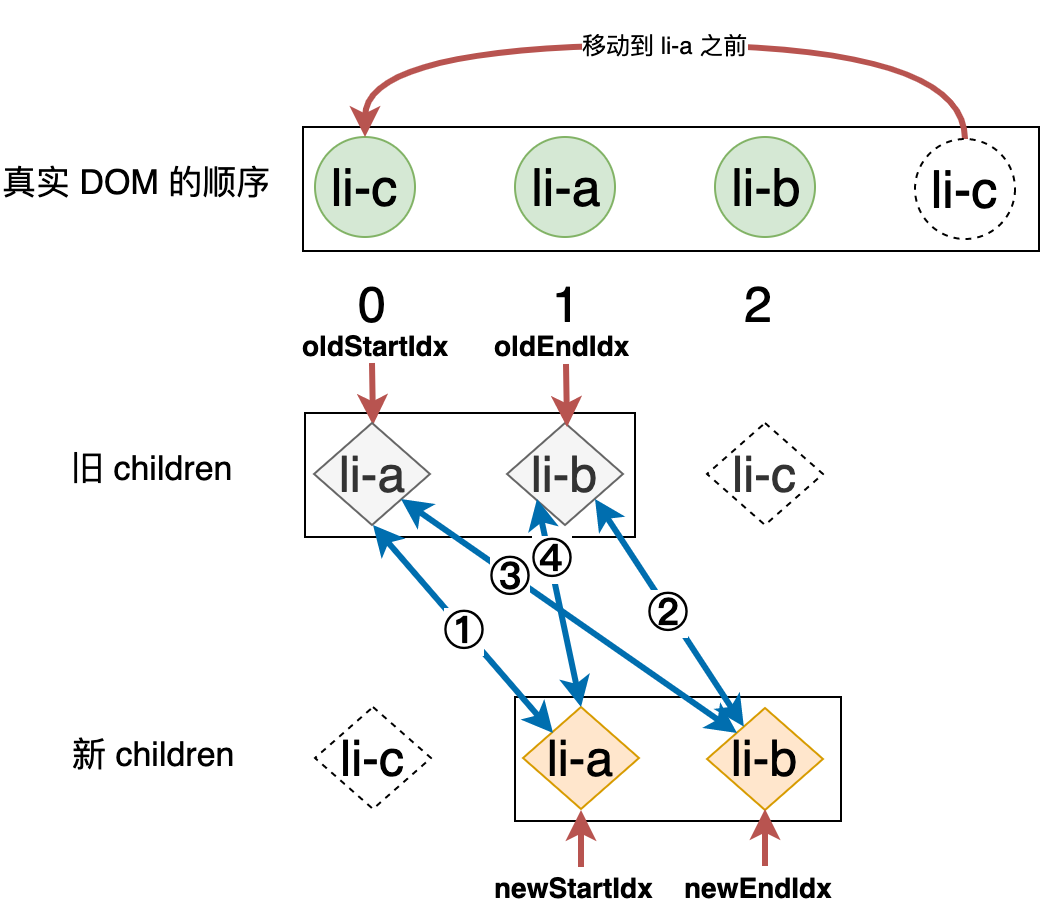
可以看到,我们只通过一次 DOM 移动,就使得真实 DOM 的顺序与新 children 中节点的顺序一致,完成了更新。换句话说,双端比较在移动 DOM 方面更具有普适性,不会因为 DOM 结构的差异而产生影响。
# 非理想情况的处理方式
在之前的讲解中,我们所采用的是较理想的例子,换句话说,在每一轮的比对过程中,总会满足四个步骤中的一步,但实际上大多数情况下并不会这么理想,如下图所示:
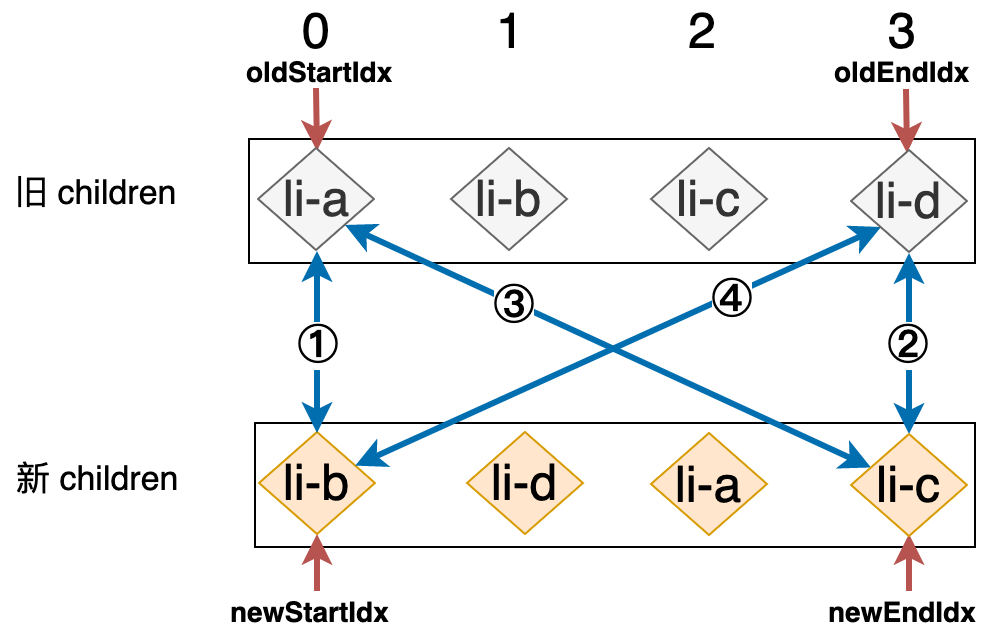
上图中 ①、②、③、④ 这四步中的每一步比对,都无法找到可复用的节点,这时应该怎么办呢?没办法,我们只能拿新 children 中的第一个节点尝试去旧 children 中寻找,试图找到拥有相同 key 值的节点,如下高亮代码所示:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (oldStartVNode.key === newStartVNode.key) {
// 省略...
} else if (oldEndVNode.key === newEndVNode.key) {
// 省略...
} else if (oldStartVNode.key === newEndVNode.key) {
// 省略...
} else if (oldEndVNode.key === newStartVNode.key) {
// 省略...
} else {
// 遍历旧 children,试图寻找与 newStartVNode 拥有相同 key 值的元素
const idxInOld = prevChildren.findIndex(
node => node.key === newStartVNode.key
)
}
}
这段代码增加了 else 分支,用来处理在四个步骤的比对中都没有成功的情况,我们遍历了旧的 children,并试图找到与新 children 中第一个节点拥有相同 key 值的节点,并把该节点在旧 children 中的位置索引记录下来,存储到 idxInOld 常量中。这里的关键点并不在于我们找到了位置索引,而是要明白**在旧的 children 中找到了与新 children 中第一个节点拥有相同 key 值的节点,意味着什么?**这意味着:旧 children 中的这个节点所对应的真实 DOM 在新 children 的顺序中,已经变成了第一个节点。所以我们需要把该节点所对应的真实 DOM 移动到最前头,如下图所示:
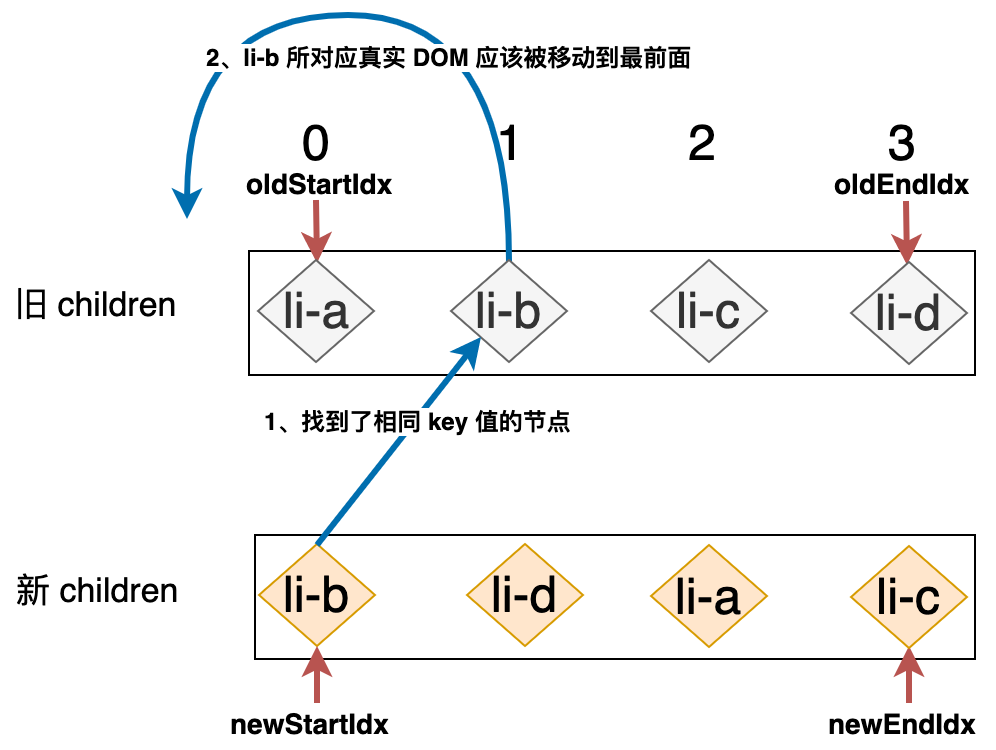
可以用如下高亮的代码来实现这个过程:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (oldStartVNode.key === newStartVNode.key) {
// 省略...
} else if (oldEndVNode.key === newEndVNode.key) {
// 省略...
} else if (oldStartVNode.key === newEndVNode.key) {
// 省略...
} else if (oldEndVNode.key === newStartVNode.key) {
// 省略...
} else {
// 遍历旧 children,试图寻找与 newStartVNode 拥有相同 key 值的元素
const idxInOld = prevChildren.findIndex(
node => node.key === newStartVNode.key
)
if (idxInOld >= 0) {
// vnodeToMove 就是在旧 children 中找到的节点,该节点所对应的真实 DOM 应该被移动到最前面
const vnodeToMove = prevChildren[idxInOld]
// 调用 patch 函数完成更新
patch(vnodeToMove, newStartVNode, container)
// 把 vnodeToMove.el 移动到最前面,即 oldStartVNode.el 的前面
container.insertBefore(vnodeToMove.el, oldStartVNode.el)
// 由于旧 children 中该位置的节点所对应的真实 DOM 已经被移动,所以将其设置为 undefined
prevChildren[idxInOld] = undefined
}
// 将 newStartIdx 下移一位
newStartVNode = nextChildren[++newStartIdx]
}
}
如果 idxInOld 存在,说明我们在旧 children 中找到了相应的节点,于是我们拿到该节点,将其赋值给 vnodeToMove 常量,意味着该节点是需要被移动的节点,同时调用 patch 函数完成更新,接着将该节点所对应的真实 DOM 移动到最前面,也就是 oldStartVNode.el 前面,由于该节点所对应的真实 DOM 已经被移动,所以我们将该节点置为 undefined,这是很关键的异步,最后我们将 newStartIdx 下移一位,准备进行下一轮的比较。我们用一张图来描述这个过程结束之后的状态:
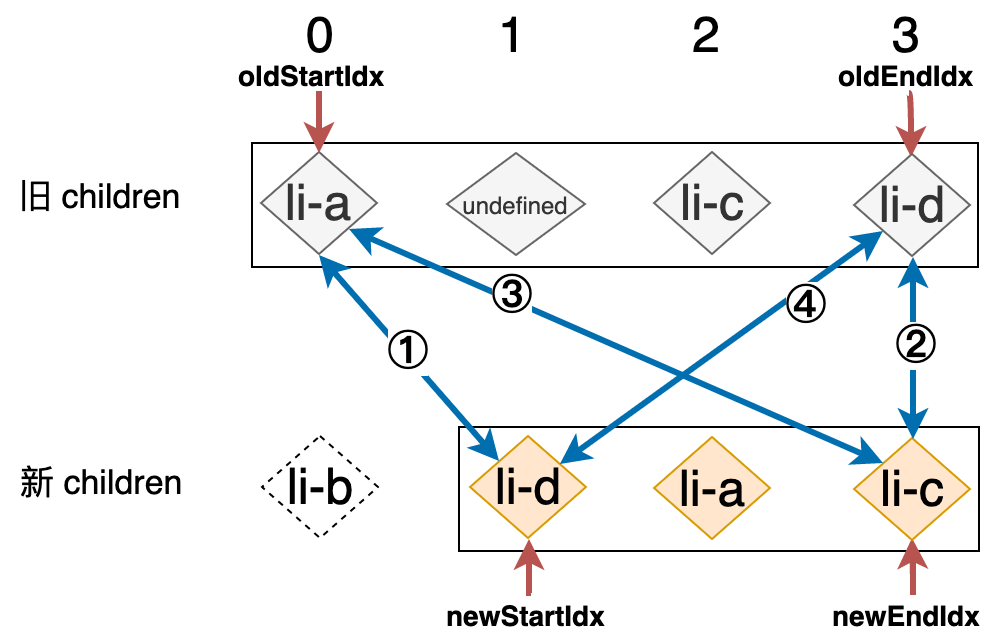
这里大家需要注意,由上图可知,由于原本旧 children 中的 li-b 节点,此时已经变成了 undefined,所以在后续的比对过程中 oldStartIdx 或 oldEndIdx 二者当中总会有一个位置索引优先达到这个位置,也就是说此时 oldStartVNode 或 oldEndVNode 两者之一可能是 undefined,这说明该位置的元素在之前的比对中被移动到别的位置了,所以不再需要处理该位置的节点,这时我们需要跳过这一位置,所以我们需要增加如下高亮代码来完善我们的算法:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (!oldStartVNode) {
oldStartVNode = prevChildren[++oldStartIdx]
} else if (!oldEndVNode) {
oldEndVNode = prevChildren[--oldEndIdx]
} else if (oldStartVNode.key === newStartVNode.key) {
// 省略...
} else if (oldEndVNode.key === newEndVNode.key) {
// 省略...
} else if (oldStartVNode.key === newEndVNode.key) {
// 省略...
} else if (oldEndVNode.key === newStartVNode.key) {
// 省略...
} else {
const idxInOld = prevChildren.findIndex(
node => node.key === newStartVNode.key
)
if (idxInOld >= 0) {
const vnodeToMove = prevChildren[idxInOld]
patch(vnodeToMove, newStartVNode, container)
prevChildren[idxInOld] = undefined
container.insertBefore(vnodeToMove.el, oldStartVNode.el)
}
newStartVNode = nextChildren[++newStartIdx]
}
}
当 oldStartVNode 或 oldEndVNode 不存在时,说明该节点已经被移动了,我们只需要跳过该位置即可。以上就是我们所说的双端比较的非理想情况的处理方式。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/vjp265qxnl (opens new window)
# 添加新元素
在上一小节中,我们尝试拿着新 children 中的第一个节点去旧 children 中寻找与之拥有相同 key 值的可复用节点,然后并非总是能够找得到,当新的 children 中拥有全新的节点时,就会出现找不到的情况,如下图所示:
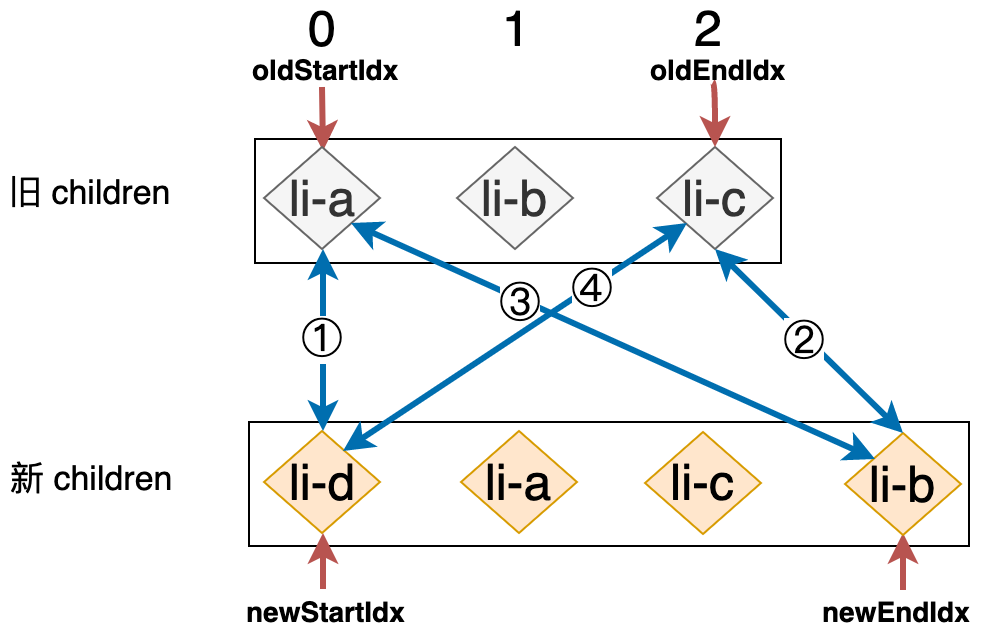
在新 children 中,节点 li-d 是一个全新的节点。在这个例子中 ①、②、③、④ 这四步的比对仍然无法找到可复用节点,所以我们会尝试拿着新 children 中的 li-d 节点去旧的 children 寻找与之拥有相同 key 值的节点,结果很显然,我们无法找到这样的节点。这时说明该节点是一个全新的节点,我们应该将其挂载到容器中,不过应该将其挂载到哪里呢?稍作分析即可得出结论,由于 li-d 节点的位置索引是 newStartIdx,这说明 li-d 节点是当前这一轮比较中的“第一个”节点,所以只要把它挂载到位于 oldStartIdx 位置的节点所对应的真实 DOM 前面就可以了,即 oldStartVNode.el,我们只需要增加一行代码即可实现该功能:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (!oldStartVNode) {
oldStartVNode = prevChildren[++oldStartIdx]
} else if (!oldEndVNode) {
oldEndVNode = prevChildren[--oldEndIdx]
} else if (oldStartVNode.key === newStartVNode.key) {
// 省略...
} else if (oldEndVNode.key === newEndVNode.key) {
// 省略...
} else if (oldStartVNode.key === newEndVNode.key) {
// 省略...
} else if (oldEndVNode.key === newStartVNode.key) {
// 省略...
} else {
const idxInOld = prevChildren.findIndex(
node => node.key === newStartVNode.key
)
if (idxInOld >= 0) {
const vnodeToMove = prevChildren[idxInOld]
patch(vnodeToMove, newStartVNode, container)
prevChildren[idxInOld] = undefined
container.insertBefore(vnodeToMove.el, oldStartVNode.el)
} else {
// 使用 mount 函数挂载新节点
mount(newStartVNode, container, false, oldStartVNode.el)
}
newStartVNode = nextChildren[++newStartIdx]
}
}
如上高亮代码所示,如果条件 idxInOld >= 0 不成立,则说明 newStartVNode 是一个全新的节点,我们添加了 else 语句块用来处理全新的节点,在 else 语句块内调用 mount 函数挂载该全新的节点,根据上面的分析,我们只需要把该节点挂载到 oldStartVNode.el 之前即可,所以我们传递给 mount 函数的第四个参数就是 oldStartVNode.el。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/n7y46ojv4m (opens new window)
但这么做真的就完美了吗?不是的,来看下面这个例子,我们更换新 children 中节点的顺序,如下图所示:
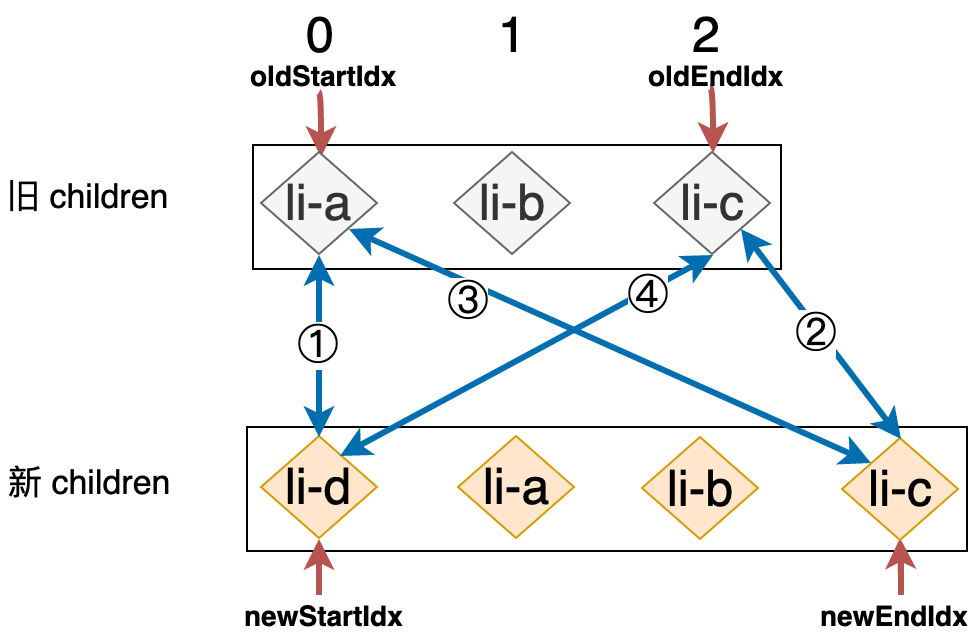
与之前的案例不同,在之前的案例中新 children 中节点的顺序为 li-d、li-a、li-c 最后是 li-b,我们观察上图可以发现,本例中新 children 的节点顺序为 li-d、li-a、li-b 最后是 li-c,那么顺序的不同会对结果产生影响吗?想弄明白这个问题很简单,我们只需要按照双端比较算法的思路来模拟执行一次即可得出结论:
- 第一步:拿旧
children中的li-a和新children中的li-d进行比对,由于二者key值不同,所以不可复用,什么都不做。 - 第二步:拿旧
children中的li-c和新children中的li-c进行比对,此时,二者拥有相同的key值。
在第二步中找到了可复用节点,接着使用 patch 函数对该节点进行更新,同时将相应的位置索引下移一位,如下图所示:
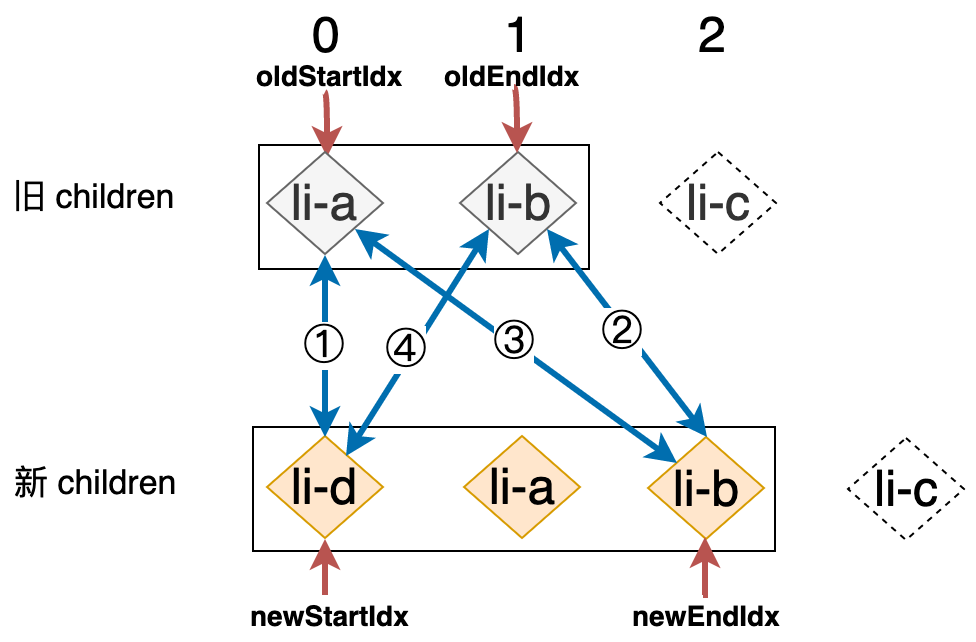
接着,开始下一轮的比较,重新从第一步开始。结果和上一轮相似,同样在第二步中找到可复用的节点,所以在在这一轮的更新完成之后,其状态如下图所示:
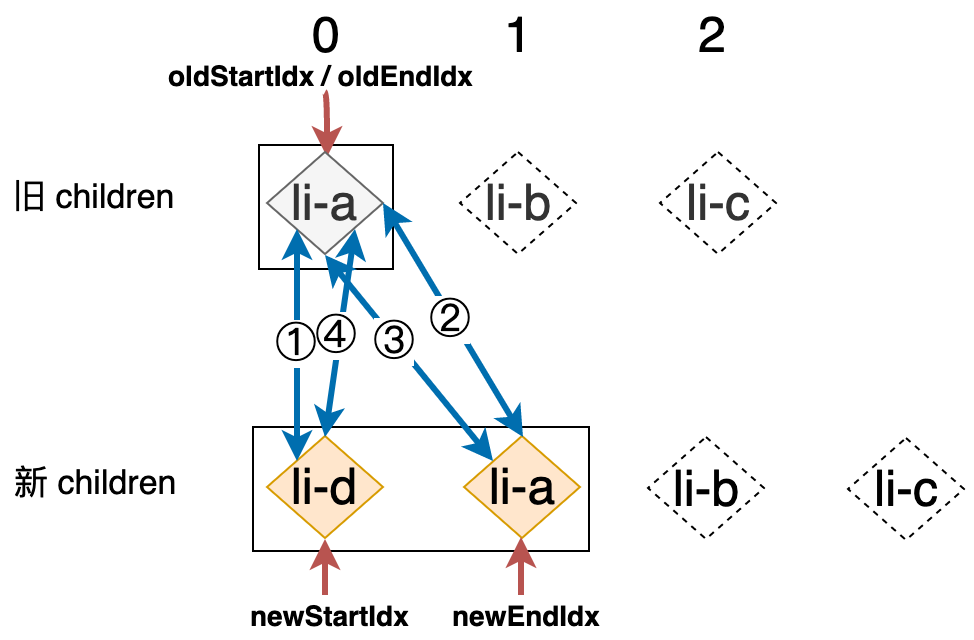
由上图可知,此时的 oldStartIdx 与 oldEndIdx 已经重合,它们的值都是 0,但是此时仍然满足循环条件,所以比对不会停止,会继续下一轮的比较。在新的一轮比较中,仍然会在第二步找到可复用的节点,所以在这一轮更新完成之后 oldEndIdx 将比 oldStartIdx 的值要小,如下图所示:
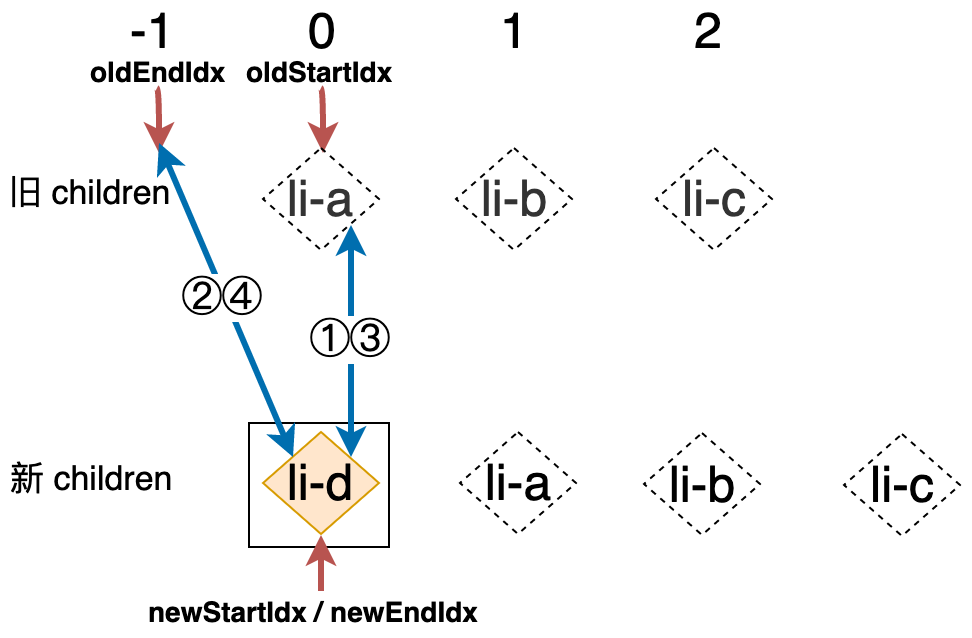
此时 oldEndIdx 的值将变成 -1,它要小于 oldStartIdx 的值,这时循环的条件不在满足,意味着更新完成。然而通过上图可以很容易的发现 li-d 节点被遗漏了,它没有得到任何的处理,通过这个案例我们意识到了之前的算法是存在缺陷的,为了弥补这个缺陷,我们需要在循环终止之后,对 oldEndIdx 和 oldStartIdx 的值进行检查,如果在循环结束之后 oldEndIdx 的值小于 oldStartIdx 的值则说明新的 children 中存在还没有被处理的全新节点,这时我们应该调用 mount 函数将其挂载到容器元素中,观察上图可知,我们只需要把这些全新的节点添加到 oldStartIdx 索引所指向的节点之前即可,如下高亮代码所示:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 省略...
}
if (oldEndIdx < oldStartIdx) {
// 添加新节点
for (let i = newStartIdx; i <= newEndIdx; i++) {
mount(nextChildren[i], container, false, oldStartVNode.el)
}
}
我们在循环结束之后,立即判断 oldEndIdx 的值是否小于 oldStartIdx 的值,如果条件成立,则需要使用 for 循环把所有位于 newStartIdx 到 newEndIdx 之间的元素都当做全新的节点添加到容器元素中,这样我们就完整的实现了完整的添加新节点的功能。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/ryryx6n42m (opens new window)
# 移除不存在的元素
对于双端比较,最后一个需要考虑的情况是:当有元素被移除时的情况,如下图所示:
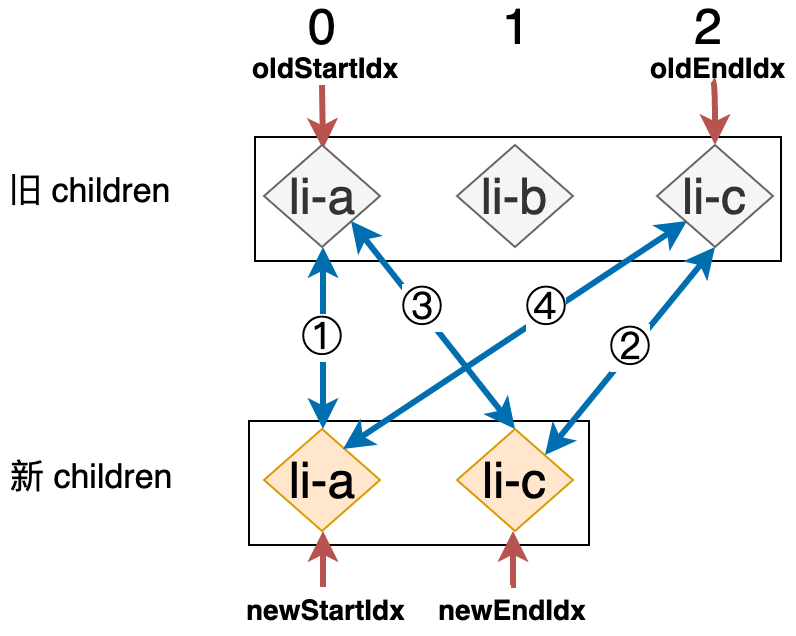
观察上图可以发现,在新 children 中 li-b 节点已经不存在了,所以完整的更新过程应该包含:移除已不存在节点所对应真实 DOM 的功能。为了找到哪些节点需要移除,我们首先还是按照双端比较的算法步骤模拟执行一下即可:
- 第一步:拿旧
children中的li-a和新children中的li-a进行比对,此时,二者拥有相同的key值。
在第一轮的第一步比对中,我们就找到了可复用节点,所以此时会调用 patch 函数更新该节点,并更新相应的索引值,可以用下图表示这一轮更新完成之后算法所处的状态:
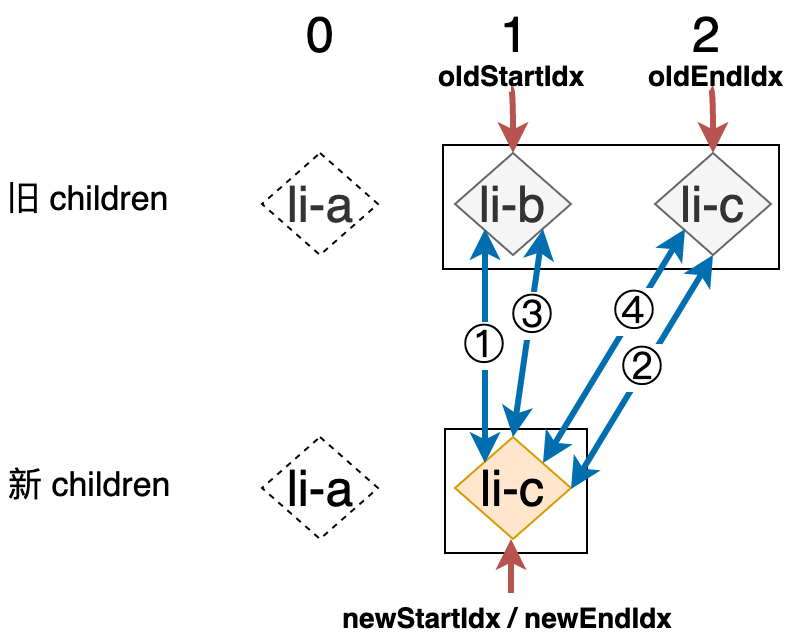
这时 newStartIdx 和 newEndIdx 的值相等,都是 1,不过循环的条件仍然满足,所以会立即进行下一轮比较:
- 第一步:拿旧
children中的li-b和新children中的li-c进行比对,由于二者key值不同,所以不可复用,什么都不做。 - 第二步:拿旧
children中的li-c和新children中的li-c进行比对,此时,二者拥有相同的key值。
在第二步的比对中找到了可复用节点 li-c,接着更新该节点,并将 oldEndIdx 和 newEndIdx 分别前移一位,最终结果如下:
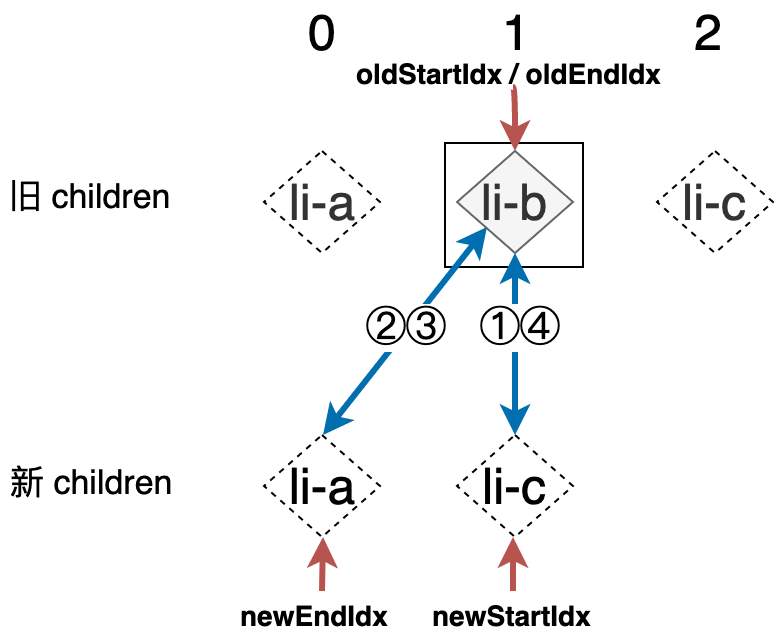
由于此时 newEndIdx 的值小于 newStartIdx 的值,所以循环将终止,但是通过上图可以发现,旧 children 中的 li-b 节点没有得到被处理的机会,我们应该将其移除才行,然后本次循环结束之后并不满足条件 oldEndIdx < oldStartIdx 而是满足条件 newEndIdx < newStartIdx,基于此,我们可以认为循环结束后,一旦满足条件 newEndIdx < newStartId 则说明有元素需要被移除。我们增加如下代码来实现该功能:
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 省略...
}
if (oldEndIdx < oldStartIdx) {
// 添加新节点
for (let i = newStartIdx; i <= newEndIdx; i++) {
mount(nextChildren[i], container, false, oldStartVNode.el)
}
} else if (newEndIdx < newStartIdx) {
// 移除操作
for (let i = oldStartIdx; i <= oldEndIdx; i++) {
container.removeChild(prevChildren[i].el)
}
}
如上高亮代码所示,增加 else...if 语句块,用来处理当 newEndIdx < newStartIdx 时的情况,我们同样开启一个 for 循环,把所有位于 oldStartIdx 和 oldEndIdx 之间的节点所对应的真实 DOM 全部移除即可。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/9jnvjj1mko (opens new window)
以上就是相对完整的双端比较算法的实现,这是 Vue2 所采用的算法,借鉴于开源项目:snabbdom (opens new window),但最早采用双端比较算法的库是 citojs (opens new window)。
# inferno 所采用的核心 Diff 算法及原理
在 Vue3 中将采用另外一种核心 Diff 算法,它借鉴于 ivi (opens new window) 和 inferno (opens new window),看下图:
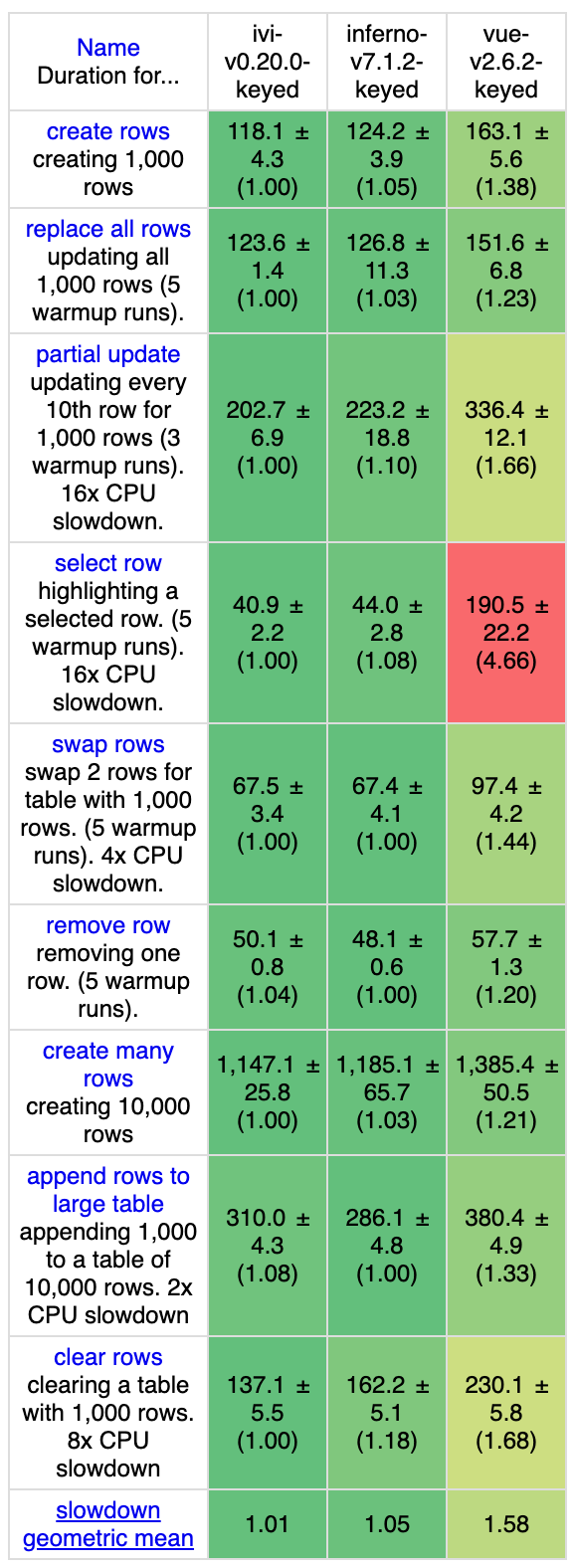
这张图来自 js-framework-benchmark (opens new window),从上图中可以看到,在 DOM 操作的各个方面,ivi 和 inferno 都要稍优于 vue2 的双端比较。但总体上的性能表现并不是单纯的由核心 Diff 算法来决定的,我们在前面章节的讲解中已经了解到的了一些优化手段,例如在创建 VNode 时就确定其类型,以及在 mount/patch 的过程中采用位运算来判断一个 VNode 的类型,在这个基础之上再配合核心的 Diff 算法,才使得性能上产生一定的优势,这也是 Vue3 接纳这种算法的原因之一,本节我们就着重讨论该核心 Diff 算法的实现原理。
# 相同的前置和后置元素
实际上本节介绍的 Diff 算法最早应用于两个不同文本之间的差异比较,在文本 Diff 中,真正进行核心的 Diff 算法之前,会有一个预处理的过程,例如可以先对两个文本进行“相等”比较:
if (text1 === text2) return
如果两个文本相等,则无需进行真正的 Diff,预处理的好处之一就是在某些情况下能够避免 Diff 算法的执行,还有比这更加高效的方式吗?当然,这是一个简单的情形,除此之外,在文本的 Diff 中还有其他的预处理过程,其中就包含:去除相同的前缀和后缀。什么意思呢?假设我们有如下两个文本:
TEXT1: I use vue for app development
text2: I use react for app development
我们通过肉眼可以很容易的发现,这两段文本头部和尾部分别有一段相同的文本:

所以真正需要进行 Diff 的部分就变成了:
text1: vue
text2: react
这么做的好处是:在某些情况下,我们能够轻松的判断出单独的文本插入和删除,例如下面的例子:
text1: I like you
text2: I like you too
这两个文本在经过去除相同的前缀和后缀之后将变成:
text1:
text2: too
所以当预处理结束之后,如果 text1 为空且 text2 不为空,则可以认为这是一个文本插入,相反的,如果将这两个文本互换位置就是一个文本删除的案例:
text1: I like you too
text2: I like you
则经过预处理之后将变成:
text1: too
text2:
这代表文本被删除。
很显然,该预处理过程在上例的情况下能够避免 Diff 算法的执行,从而提高 Diff 效率。当然,换一个角度来看的话,这本身也是 Diff 策略的一部分,不过这显然要更高效。所以我们能否将此预处理步骤应用到 VNode 的 Diff 中呢?当然可以,来看下面的例子:
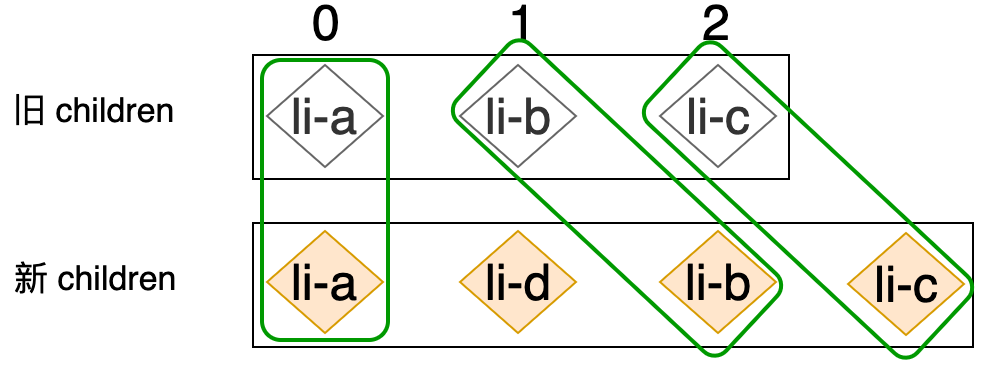
如上图所示,新旧 children 拥有相同的前缀节点和后缀节点,对于前缀节点,我们可以建立一个索引,指向新旧 children 中的第一个节点,并逐步向后遍历,直到遇到两个拥有不同 key 值的节点为止,如下代码所示:
// 更新相同的前缀节点
// j 为指向新旧 children 中第一个节点的索引
let j = 0
let prevVNode = prevChildren[j]
let nextVNode = nextChildren[j]
// while 循环向后遍历,直到遇到拥有不同 key 值的节点为止
while (prevVNode.key === nextVNode.key) {
// 调用 patch 函数更新
patch(prevVNode, nextVNode, container)
j++
prevVNode = prevChildren[j]
nextVNode = nextChildren[j]
}
可以用下图描述这一步操作完成之后的状态:
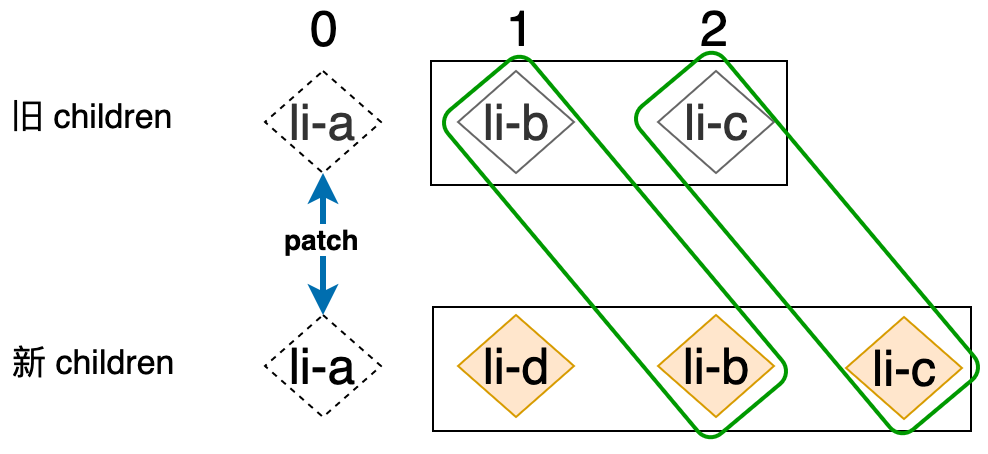
这里大家需要注意的是,当 while 循环终止时,索引 j 的值为 1。接着,我们需要处理的是相同的后缀节点,由于新旧 children 中节点的数量可能不同,所以我们需要两个索引分别指向新旧 children 的最后一个节点,并逐步向前遍历,直到遇到两个拥有不同 key 值的节点为止,如下代码所示:
// 更新相同的后缀节点
// 指向旧 children 最后一个节点的索引
let prevEnd = prevChildren.length - 1
// 指向新 children 最后一个节点的索引
let nextEnd = nextChildren.length - 1
prevVNode = prevChildren[prevEnd]
nextVNode = nextChildren[nextEnd]
// while 循环向前遍历,直到遇到拥有不同 key 值的节点为止
while (prevVNode.key === nextVNode.key) {
// 调用 patch 函数更新
patch(prevVNode, nextVNode, container)
prevEnd--
nextEnd--
prevVNode = prevChildren[prevEnd]
nextVNode = nextChildren[nextEnd]
}
可以用下图来表示这一步更新完成之后的状态:
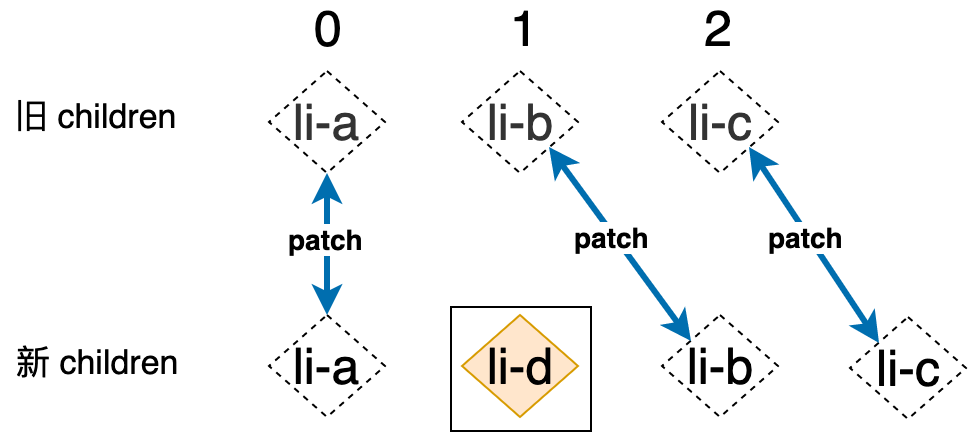
同样需要注意的是,在这一步更新完成之后 prevEnd 的值为 0,nextEnd 的值为 1。实际上三个索引 j、prevEnd 和 nextEnd 的值至关重要,它们之间的大小关系反映了新旧 children 的节点状况。前面我们在讲解文本 Diff 的时候曾说过,当“去掉”相同的前缀和后缀之后,如果旧文本为空,且新文本不为空,则说明有新的文本内容被添加,反之则说明有旧的文本被移除。现在三个索引的值如下:
j: 1
prevEnd: 0
nextEnd: 1
我们发现 j > prevEnd 并且 j <= nextEnd,这说明当新旧 children 中相同的前缀和后缀被更新之后,旧 children 中的节点已经被更新完毕了,而新 children 中仍然有剩余节点,通过上图可以发现,新 children 中的 li-d 节点,就是这个剩余的节点。实际上新 children 中位于 j 到 nextEnd 之间的所有节点都应该是新插入的节点:
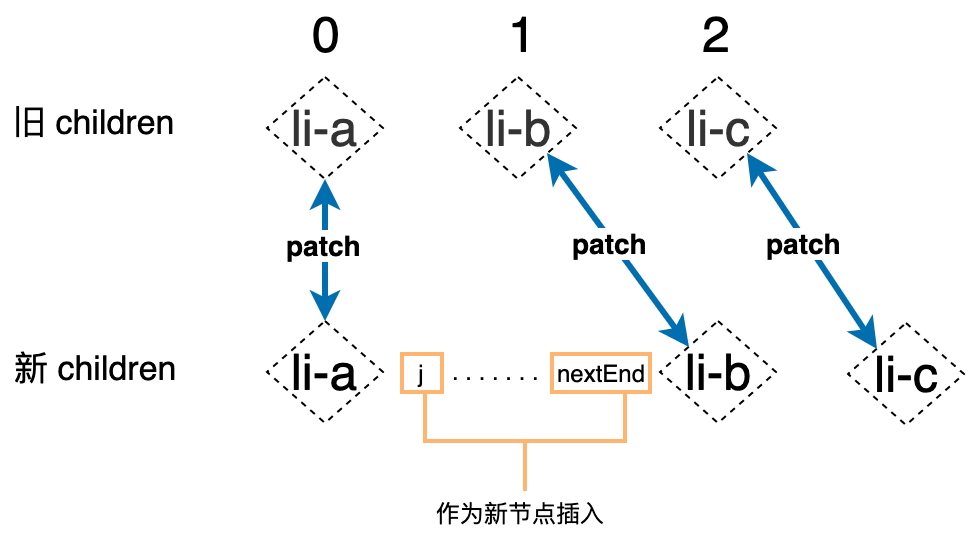
那么应该将这些新的节点插入到什么位置呢?观察上图,从新 children 中的节点顺序可以发现,新的节点都出现在 li-b 节点的前面,所以我们可以使用一个循环遍历索引 j -> nextEnd 之间的节点,并逐个将其插入到 li-b 节点之前,这样当循环结束之后,新的节点就被插入到了正确的位置。我们还能发现 li-b 节点的位置可以用 nextEnd + 1 表示,最终我们可以使用如下代码来实现节点的插入:
// 满足条件,则说明从 j -> nextEnd 之间的节点应作为新节点插入
if (j > prevEnd && j <= nextEnd) {
// 所有新节点应该插入到位于 nextPos 位置的节点的前面
const nextPos = nextEnd + 1
const refNode =
nextPos < nextChildren.length ? nextChildren[nextPos].el : null
// 采用 while 循环,调用 mount 函数挂载节点
while (j <= nextEnd) {
mount(nextChildren[j++], container, false, refNode)
}
}
再来看如下案例:
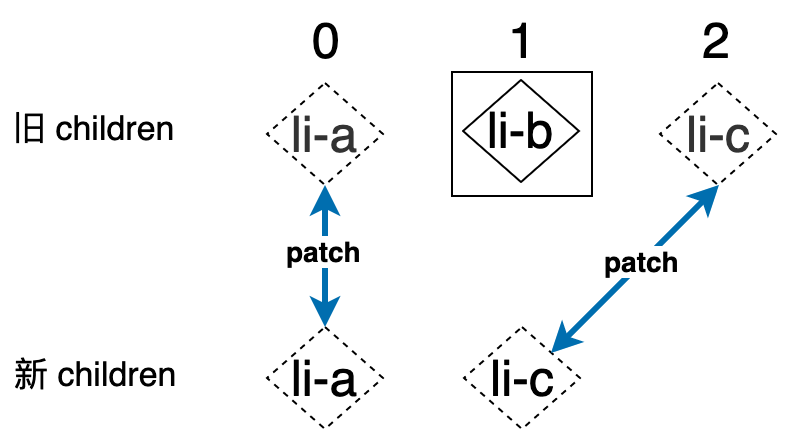
在这个案例中,当“去掉”相同的前缀和后缀之后,三个索引的值为:
j: 1
prevEnd: 1
nextEnd: 0
这时条件 j > nextEnd 并且 j <= prevEnd 成立,通过上图可以很容的发现,旧 children 中的 li-b 节点应该被移除,实际上更加通用的规则应该是:在旧 children 中有位于索引 j 到 prevEnd 之间的节点,都应该被移除。如下图所示:
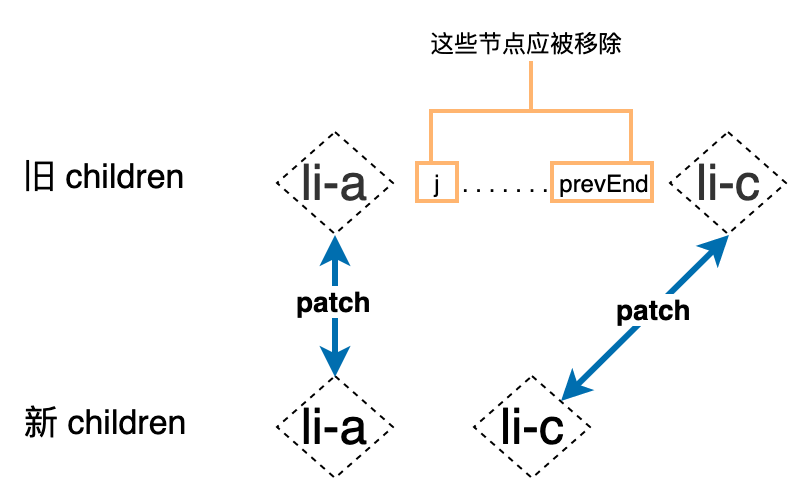
代码实现起来也很简单,如下高亮代码所示:
if (j > prevEnd && j <= nextEnd) {
// j -> nextEnd 之间的节点应该被添加
const nextPos = nextEnd + 1
const refNode =
nextPos < nextChildren.length ? nextChildren[nextPos].el : null
while (j <= nextEnd) {
mount(nextChildren[j++], container, false, refNode)
}
} else if (j > nextEnd) {
// j -> prevEnd 之间的节点应该被移除
while (j <= prevEnd) {
container.removeChild(prevChildren[j++].el)
}
}
现在我们来观察一下总体的代码结构:
// while 循环向后遍历,直到遇到拥有不同 key 值的节点为止
while (prevVNode.key === nextVNode.key) {
// 调用 patch 函数更新
// 省略...
j++
// 省略...
}
// while 循环向前遍历,直到遇到拥有不同 key 值的节点为止
while (prevVNode.key === nextVNode.key) {
// 调用 patch 函数更新
// 省略...
prevEnd--
nextEnd--
// 省略...
}
// 满足条件,则说明从 j -> nextEnd 之间的节点应作为新节点插入
if (j > prevEnd && j <= nextEnd) {
// j -> nextEnd 之间的节点应该被添加
// 省略...
} else if (j > nextEnd) {
// j -> prevEnd 之间的节点应该被移除
// 省略...
}
观察如上高亮的代码,我们发现,在两个 while 循环中,索引 j 和 索引 prevEnd、nextEnd 是以“从两端向中间靠拢”的趋势在变化的,而在两个 while 循环结束之后,我们会根据这三个索引的大小关系来决定应该做什么样的操作。现在我们思考一个问题,假设在第一个 while 循环结束之后,索引 j 的值已经大于 prevEnd 或 nextEnd,那么还有必须执行第二个 while 循环吗?答案是没有必要,这是因为一旦索引 j 大于 prevEnd 则说明旧 children 中的所有节点都已经参与了 patch,类似的,如果索引 j 大于 nextEnd 则说明新 children 中的所有节点都已经参与了 patch,这时当然没有必要再执行后续的操作了。所以出于性能的考虑,我们应该避免没有必要的代码执行,为了达到目的,可以使用 javascript 中的 label 语句,如下高亮代码所示:
outer: {
while (prevVNode.key === nextVNode.key) {
patch(prevVNode, nextVNode, container)
j++
if (j > prevEnd || j > nextEnd) {
break outer
}
prevVNode = prevChildren[j]
nextVNode = nextChildren[j]
}
// 更新相同的后缀节点
prevVNode = prevChildren[prevEnd]
nextVNode = nextChildren[nextEnd]
while (prevVNode.key === nextVNode.key) {
patch(prevVNode, nextVNode, container)
prevEnd--
nextEnd--
if (j > prevEnd || j > nextEnd) {
break outer
}
prevVNode = prevChildren[prevEnd]
nextVNode = nextChildren[nextEnd]
}
}
我们定义了 label 名字为 outer 的 label 语句块,并分别在两个 while 循环中添加了判断语句,无论在哪个循环中,只要索引 j 的值大于了 prevEnd 或 nextEnd 二者之一,我们就 break 该语句块,从而避免了无用的代码执行。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/5yo3z824vp (opens new window)
# 判断是否需要进行 DOM 移动
刚刚我们讲解了一个很重要的预处理思路:“去掉”相同的前置/后置节点。并且我们分析了在一些情况下这种预处理操作能够避免真正 Diff 算法的执行:通过判断索引的大小关系,能够提前知道哪些元素被添加,哪些元素被移除。但这毕竟属于一种特殊情况,大部分情况下可能未必如此理想,来看如下案例:
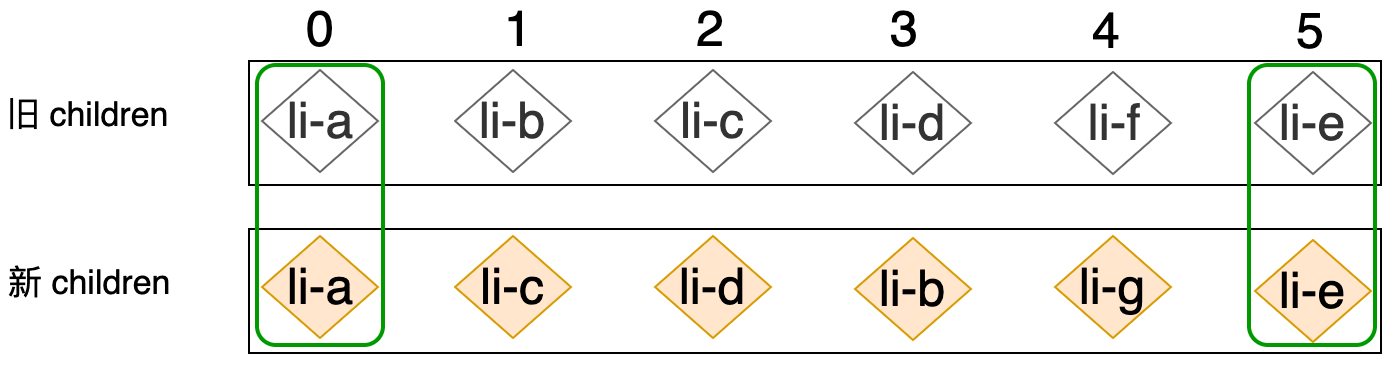
观察上图中新旧 children 中节点的顺序,我们发现,这个案例在应用预处理步骤之后,只有 li-a 节点和 li-e 节点能够被提前 patch。换句话说在这种情况下没有办法简单的通过预处理就能够结束 Diff 逻辑。这时我们就需要进行下一步操作,实际上无论是 React 的 Diff 算法,还是 Vue2(snabbdom) 的 Diff 算法,其重点无非就是:判断是否有节点需要移动,以及应该如何移动和寻找出那些需要被添加或移除的节点,而本节我们所讲解的算法也不例外,所以接下来的任务就是:判断那些节点需要移动,以及如何移动。
为了让事情更直观我们把该案例在应用预处理之后的状态用下图描述出来:
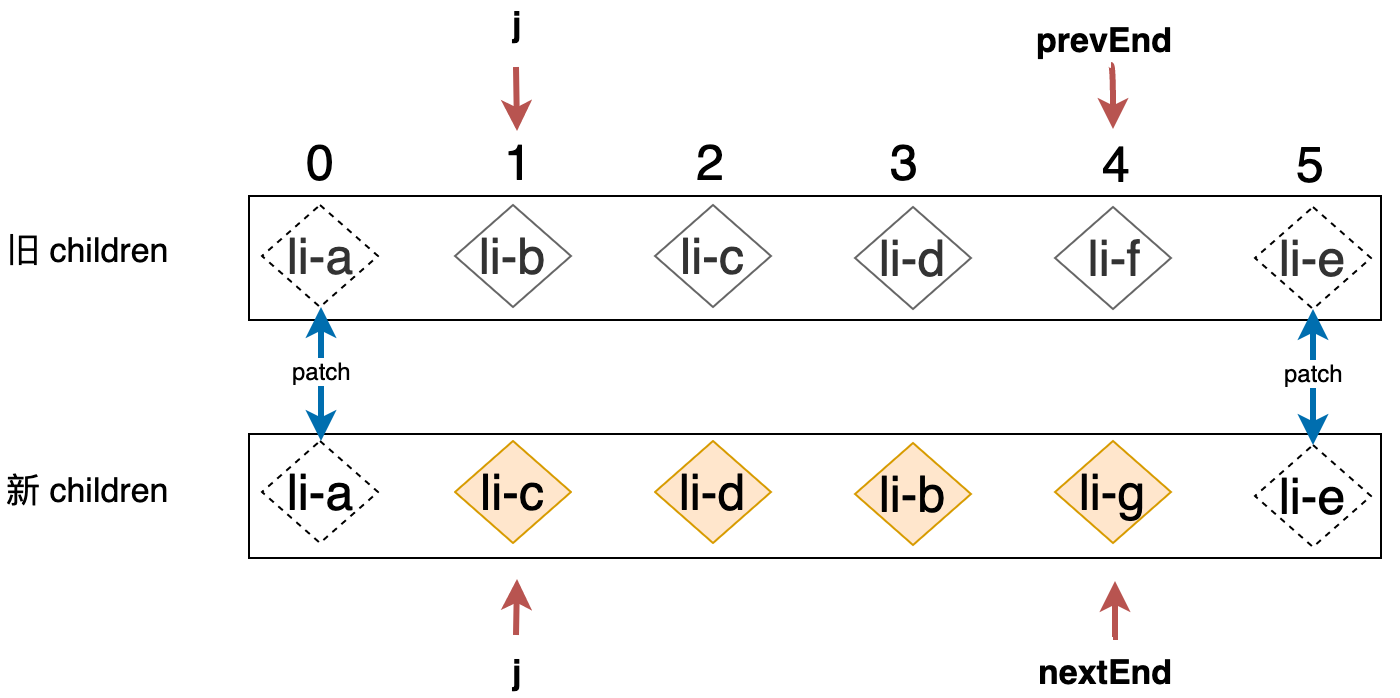
观察上图可以发现,此时索引 j 既不大于 prevEnd 也不大于 nextEnd,所以如下代码将得不到执行:
// 满足条件,则说明从 j -> nextEnd 之间的节点应作为新节点插入
if (j > prevEnd && j <= nextEnd) {
// j -> nextEnd 之间的节点应该被添加
// 省略...
} else if (j > nextEnd) {
// j -> prevEnd 之间的节点应该被移除
// 省略...
}
我们需要为这段代码添加 else 语句块,用来处理该案例的情况,如下高亮代码所示:
// 满足条件,则说明从 j -> nextEnd 之间的节点应作为新节点插入
if (j > prevEnd && j <= nextEnd) {
// j -> nextEnd 之间的节点应该被添加
// 省略...
} else if (j > nextEnd) {
// j -> prevEnd 之间的节点应该被移除
// 省略...
} else {
// 在这里编写处理逻辑
}
知道了应该在哪里编写处理逻辑,那么接下来我们就讲解一下该算法的思路。首先,我们需要构造一个数组 source,该数组的长度等于新 children 在经过预处理之后剩余未处理节点的数量,并且该数组中每个元素的初始值为 -1,如下图所示:
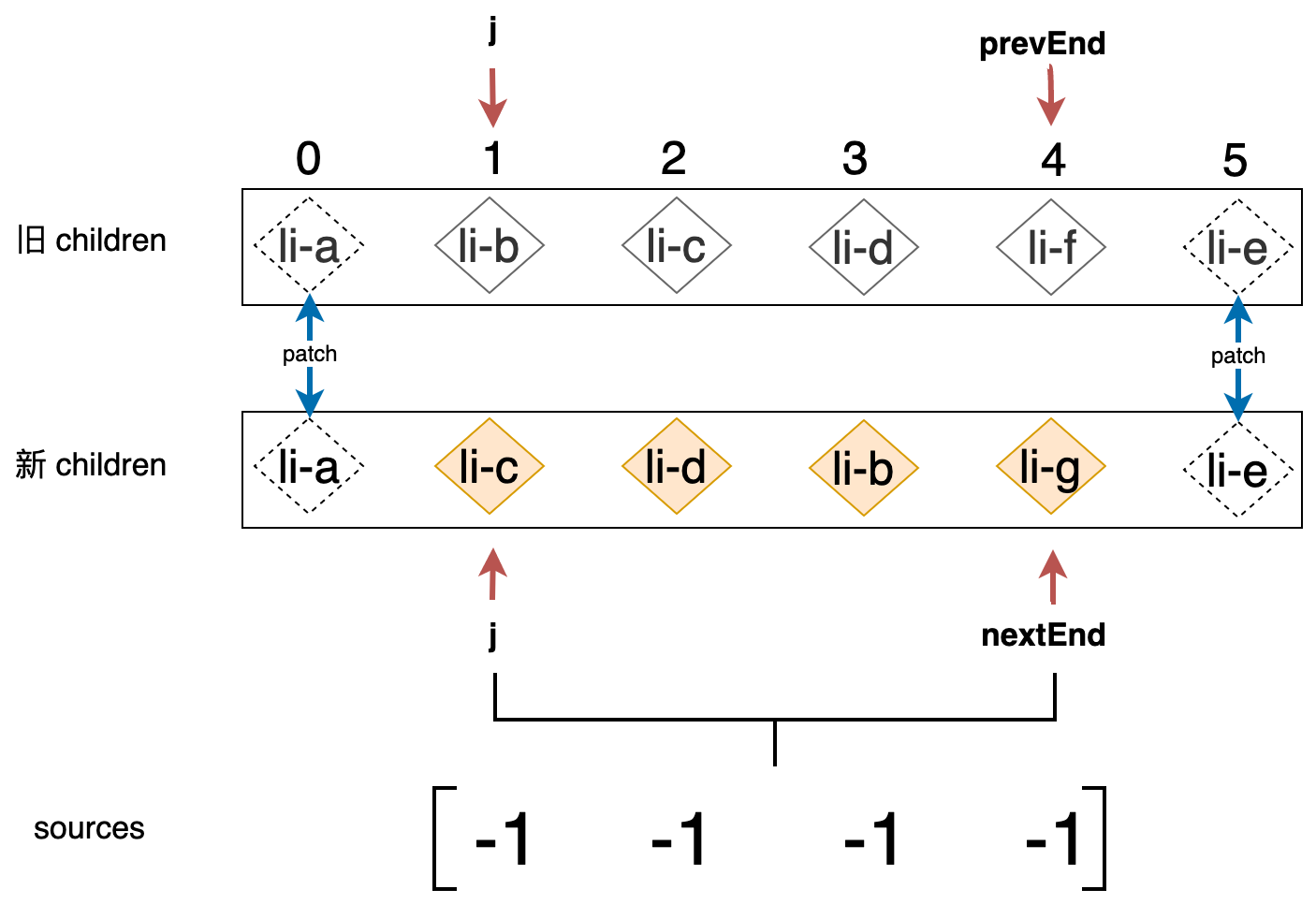
我们可以通过如下代码完成 source 数组的构造:
if (j > prevEnd && j <= nextEnd) {
// 省略...
} else if (j > nextEnd) {
// 省略...
} else {
// 构造 source 数组
const nextLeft = nextEnd - j + 1 // 新 children 中剩余未处理节点的数量
const source = []
for (let i = 0; i < nextLeft; i++) {
source.push(-1)
}
}
那么这个数组的作用是什么呢?通过上图可以发现,该数组中的每一个元素分别与新 children 中剩余未处理的节点对应,实际上 source 数组将用来存储新 children 中的节点在旧 children 中的位置,后面将会使用它计算出一个最长递增子序列,并用于 DOM 移动。如下图所示:
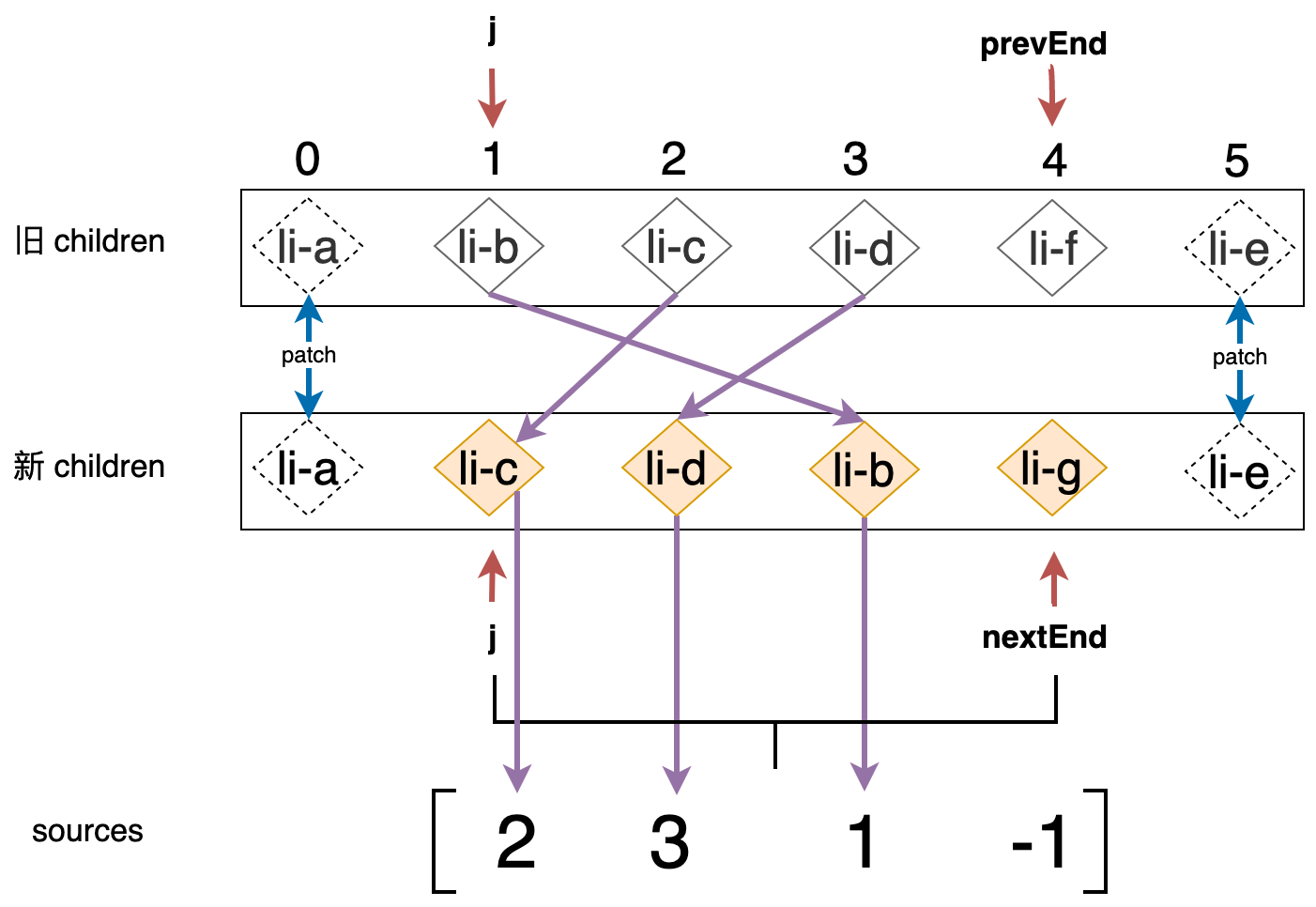
我们可以通过两层 for 循环来完成这个工作,外层循环用于遍历旧 children,内层循环用于遍历新 children:
const prevStart = j
const nextStart = j
// 遍历旧 children
for (let i = prevStart; i <= prevEnd; i++) {
const prevVNode = prevChildren[i]
// 遍历新 children
for (let k = nextStart; k <= nextEnd; k++) {
const nextVNode = nextChildren[k]
// 找到拥有相同 key 值的可复用节点
if (prevVNode.key === nextVNode.key) {
// patch 更新
patch(prevVNode, nextVNode, container)
// 更新 source 数组
source[k - nextStart] = i
}
}
}
如上代码所示,外层循环逐个从旧 children 中取出未处理的节点,并尝试在新 children 中寻找拥有相同 key 值的可复用节点,一旦找到了可复用节点,则调用 patch 函数更新之。接着更新 source 数组中对应位置的值,这里需要注意的是,由于 k - nextStart 的值才是正确的位置索引,而非 k 本身,并且外层循环中变量 i 的值就代表了该节点在旧 children 中的位置,所以直接将 i 赋值给 source[k - nextStart] 即可达到目的,最终的效果就如上图中所展示的那样。可以看到 source 数组的第四个元素值仍然为初始值 -1,这是因为新 children 中的 li-g 节点不存在于旧 children 中。除此之外,还有一件很重要的事儿需要做,即判断是否需要移动节点,判断的方式类似于 React 所采用的方式,如下高亮代码所示:
const prevStart = j
const nextStart = j
let moved = false
let pos = 0
for (let i = prevStart; i <= prevEnd; i++) {
const prevVNode = prevChildren[i]
for (let k = nextStart; k <= nextEnd; k++) {
const nextVNode = nextChildren[k]
if (prevVNode.key === nextVNode.key) {
// patch 更新
patch(prevVNode, nextVNode, container)
// 更新 source 数组
source[k - nextStart] = i
// 判断是否需要移动
if (k < pos) {
moved = true
} else {
pos = k
}
}
}
}
变量 k 代表我们在遍历新 children 中遇到的节点的位置索引,变量 pos 用来存储遇到的位置索引的最大值,一旦发现后来遇到索引比之前遇到的索引要小,即 k < pos,则说明需要移动操作,这时我们更新变量 moved 的值为 true,moved 变量将会在后面使用。
不过在进一步讲解之前,我们需要回头思考一下上面的代码存在怎样的问题?上面的代码中我们采用两层嵌套的循环,其时间复杂度为 O(n1 * n2),其中 n1 和 n2 为新旧 children 中节点的数量,我们也可以使用 O(n^2) 来表示,当新旧 children 中节点的数量较多时,则两层嵌套的循环会带来性能的问题,出于优化的目的,我们可以为新的 children 中的节点构建一个 key 到 位置索引 的索引表,如下图所示:
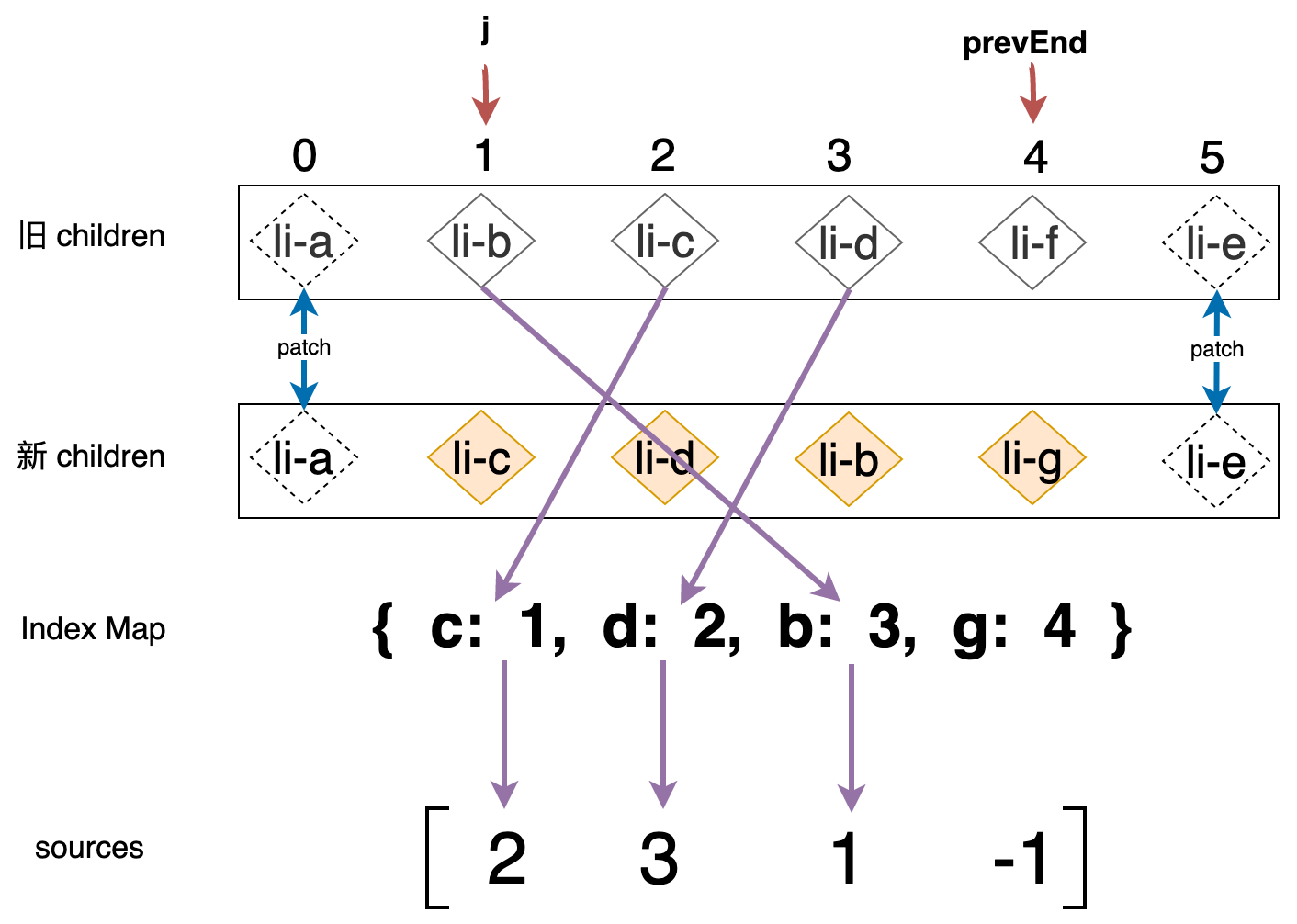
Index Map 中的键是节点的 key,值是节点在新 children 中的位置索引,由于数据结构带来的优势,使得我们能够非常快速的定位旧 children 中的节点在新 children 中的位置,落实的代码如下:
const prevStart = j
const nextStart = j
let moved = false
let pos = 0
// 构建索引表
const keyIndex = {}
for(let i = nextStart; i <= nextEnd; i++) {
keyIndex[nextChildren[i].key] = i
}
// 遍历旧 children 的剩余未处理节点
for(let i = prevStart; i <= prevEnd; i++) {
prevVNode = prevChildren[i]
// 通过索引表快速找到新 children 中具有相同 key 的节点的位置
const k = keyIndex[prevVNode.key]
if (typeof k !== 'undefined') {
nextVNode = nextChildren[k]
// patch 更新
patch(prevVNode, nextVNode, container)
// 更新 source 数组
source[k - nextStart] = i
// 判断是否需要移动
if (k < pos) {
moved = true
} else {
pos = k
}
} else {
// 没找到
}
}
这是典型的用空间换时间的方式,复杂度能够降低到 O(n)。但无论采用哪一种方式,最终我们的目的是对新旧 children 中具有相同 key 值的节点进行更新,同时检测是否需要移动操作。在如上代码执行完毕之后,如果发现变量 moved 的值为 true,则说明需要移动操作。
另外在上面的代码中,我们试图拿旧 children 中的节点尝试去新 children 中寻找具有相同 key 值的节点,但并非总是能够找得到,当 k === 'undefined' 时,说明该节点在新 children 中已经不存在了,这时我们应该将其移除,如下高亮代码所示:
// 遍历旧 children 的剩余未处理节点
for(let i = prevStart; i <= prevEnd; i++) {
prevVNode = prevChildren[i]
// 通过索引表快速找到新 children 中具有相同 key 的节点的位置
const k = keyIndex[prevVNode.key]
if (typeof k !== 'undefined') {
// 省略...
} else {
// 没找到,说明旧节点在新 children 中已经不存在了,应该移除
container.removeChild(prevVNode.el)
}
}
除此之外,我们还需要一个数量标识,用来代表已经更新过的节点的数量。我们知道,已经更新过的节点数量应该小于新 children 中需要更新的节点数量,一旦更新过的节点数量超过了新 children 中需要更新的节点数量,则说明该节点是多余的节点,我们也应该将其移除,如下高亮代码所示:
let patched = 0
// 遍历旧 children 的剩余未处理节点
for (let i = prevStart; i <= prevEnd; i++) {
prevVNode = prevChildren[i]
if (patched < nextLeft) {
// 通过索引表快速找到新 children 中具有相同 key 的节点的位置
const k = keyIndex[prevVNode.key]
if (typeof k !== 'undefined') {
nextVNode = nextChildren[k]
// patch 更新
patch(prevVNode, nextVNode, container)
patched++
// 更新 source 数组
source[k - nextStart] = i
// 判断是否需要移动
if (k < pos) {
moved = true
} else {
pos = k
}
} else {
// 没找到,说明旧节点在新 children 中已经不存在了,应该移除
container.removeChild(prevVNode.el)
}
} else {
// 多余的节点,应该移除
container.removeChild(prevVNode.el)
}
}
变量 patched 将作为数量标识,它的初始值为 0,只有当条件 patched < nextLeft 不成立时,说明该节点已经不存在与新 children 中了,是一个多余的节点,于是我们将其移除。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/03o5plkv40 (opens new window)
# DOM 移动的方式
在上一小节,我们的主要目的有两个:1、判断出是否需要进行 DOM 移动操作,所以我们建立了 moved 变量作为标识,当它的值为 true 时则说明需要进行 DOM 移动;2、构建 source 数组,它的长度与“去掉”相同的前置/后置节点后新 children 中剩余未处理节点的数量相等,并存储着新 children 中的节点在旧 children 中位置,后面我们会根据 source 数组计算出一个最长递增子序列,并用于 DOM 移动操作。如下图所示:

现在我们已经可以通过判断变量 moved 的值来确定是否需要进行 DOM 移动操作:
if (moved) {
// 如果 moved 为真,则需要进行 DOM 移动操作
}
一旦需要进行 DOM 节点的移动,我们首先要做的就是根据 source 数组计算一个最长递增子序列:
if (moved) {
// 计算最长递增子序列
const seq = lis(sources) // [ 0, 1 ]
}
TIP
什么是最长递增子序列:给定一个数值序列,找到它的一个子序列,并且子序列中的值是递增的,子序列中的元素在原序列中不一定连续。
例如给定数值序列为:[ 0, 8, 4, 12 ]
那么它的最长递增子序列就是:[0, 8, 12]
当然答案可能有多种情况,例如:[0, 4, 12] 也是可以的
TIP
我们会在下一小节讲解 lis 函数的实现。
上面的代码中,我们调用 lis 函数求出数组 source 的最长递增子序列为 [ 0, 1 ]。我们知道 source 数组的值为 [2, 3, 1, -1],很显然最长递增子序列应该是 [ 2, 3 ],但为什么计算出的结果是 [ 0, 1 ] 呢?其实 [ 0, 1 ] 代表的是最长递增子序列中的各个元素在 source 数组中的位置索引,如下图所示:
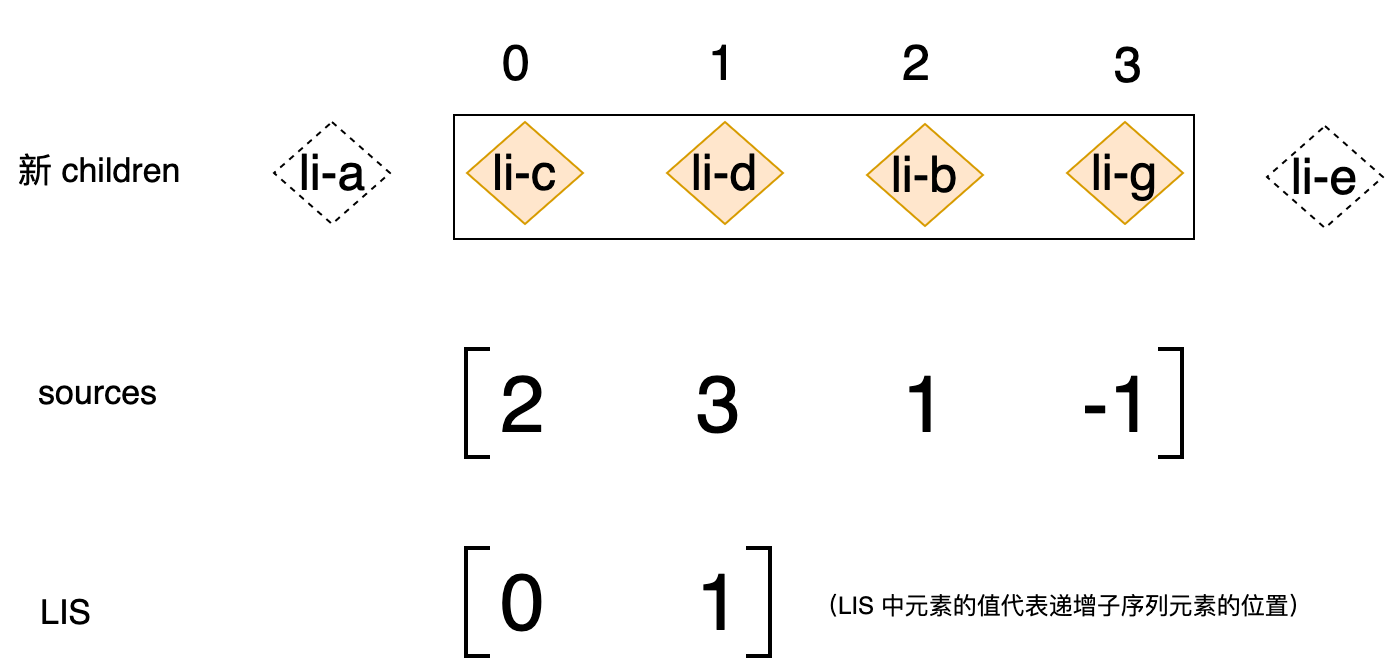
我们对新 children 中的剩余未处理节点进行了重新编号,li-c 节点的位置是 0,以此类推。而最长递增子序列是 [ 0, 1 ] 这告诉我们:新 children 的剩余未处理节点中,位于位置 0 和位置 1 的节点的先后关系与他们在旧 children 中的先后关系相同。或者我们可以理解为位于位置 0 和位置 1 的节点是不需要被移动的节点,即上图中 li-c 节点和 li-d 节点将在接下来的操作中不会被移动。换句话说只有 li-b 节点和 li-g 节点是可能被移动的节点,但是我们发现与 li-g 节点位置对应的 source 数组元素的值为 -1,这说明 li-g 节点应该作为全新的节点被挂载,所以只有 li-b 节点需要被移动。我们来看下图:
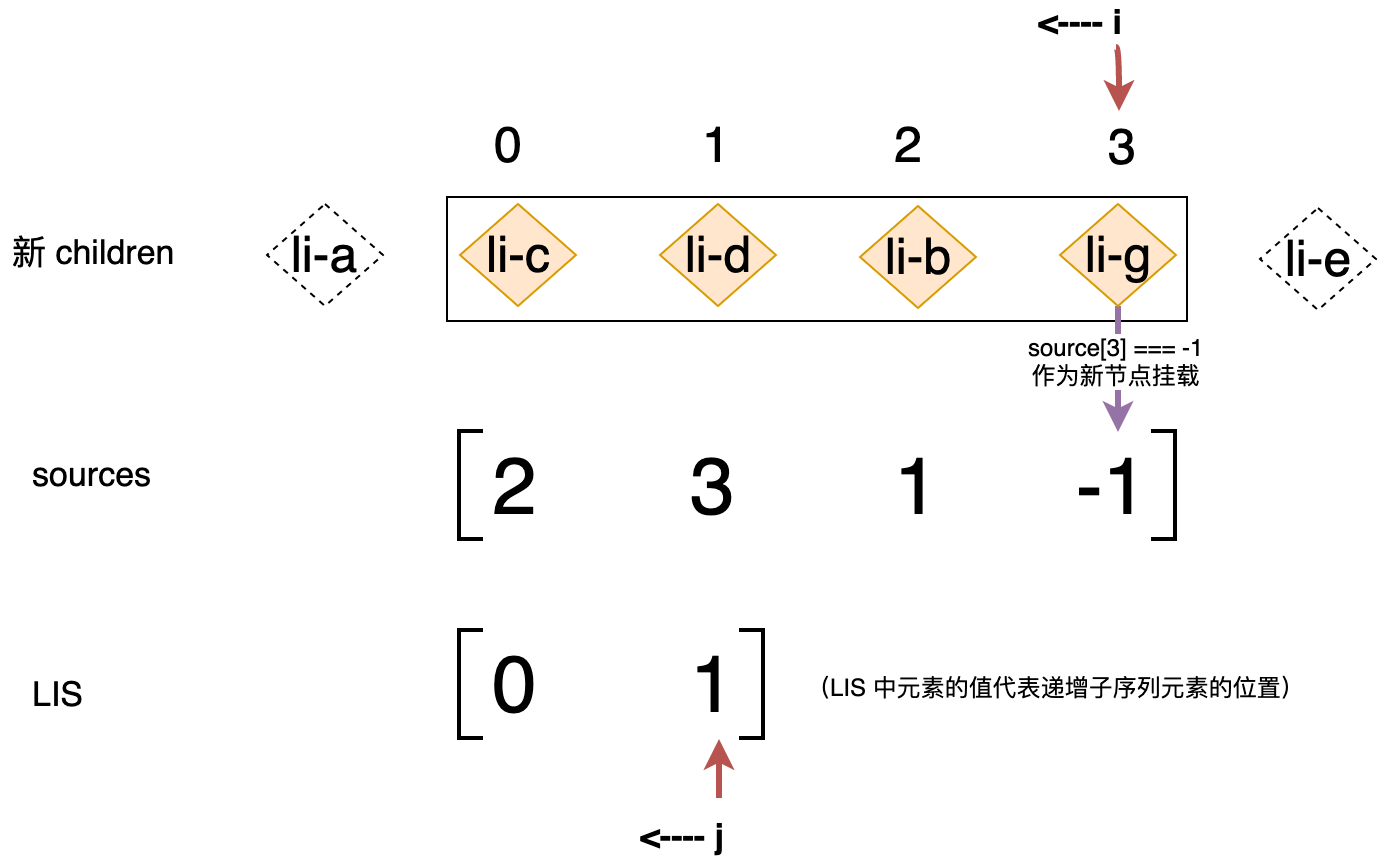
使用两个索引 i 和 j 分别指向新 children 中剩余未处理节点的最后一个节点和最长递增子序列数组中的最后一个位置,并从后向前遍历,如下代码所示:
if (moved) {
const seq = lis(source)
// j 指向最长递增子序列的最后一个值
let j = seq.length - 1
// 从后向前遍历新 children 中的剩余未处理节点
for (let i = nextLeft - 1; i >= 0; i--) {
if (i !== seq[j]) {
// 说明该节点需要移动
} else {
// 当 i === seq[j] 时,说明该位置的节点不需要移动
// 并让 j 指向下一个位置
j--
}
}
}
变量 j 指向最长递增子序列的最后一个位置,使用 for 循环从后向前遍历新 children 中剩余未处理的子节点,这里的技巧在于 i 的值的范围是 0 到 nextLeft - 1,这实际上就等价于我们对剩余节点进行了重新编号。接着判断当前节点的位置索引值 i 是否与子序列中位于 j 位置的值相等,如果不相等,则说明该节点需要被移动;如果相等则说明该节点不需要被移动,并且会让 j 指向下一个位置。但是我们观察上图可以发现 li-g 节点的位置索引是 3,它不等于 1(seq[j]),难道说明 li-g 节点需要被移动吗?其实不是,我们还可以发现与 li-g 节点位置对应的 source 数组中的元素值为 -1,这说明 li-g 节点应该作为全新的节点挂载,所以我们还需增加一个判断,优先检查一个节点是否是全新的节点:
if (moved) {
const seq = lis(source)
// j 指向最长递增子序列的最后一个值
let j = seq.length - 1
// 从后向前遍历新 children 中的剩余未处理节点
for (let i = nextLeft - 1; i >= 0; i--) {
if (source[i] === -1) {
// 作为全新的节点挂载
// 该节点在新 children 中的真实位置索引
const pos = i + nextStart
const nextVNode = nextChildren[pos]
// 该节点下一个节点的位置索引
const nextPos = pos + 1
// 挂载
mount(
nextVNode,
container,
false,
nextPos < nextChildren.length
? nextChildren[nextPos].el
: null
)
} else if (i !== seq[j]) {
// 说明该节点需要移动
} else {
// 当 i === seq[j] 时,说明该位置的节点不需要移动
// 并让 j 指向下一个位置
j--
}
}
}
如上代码的关键在于,为了将节点挂载到正确的位置,我们需要找到当前节点的真实位置索引(i + nextStart),以及当前节点的后一个节点,并挂载该节点的前面即可。这样我们就完成了 li-g 节点的挂载。接着循环会继续执行,索引 i 将指向下一个位置,即指向 li-b 节点,如下图所示:
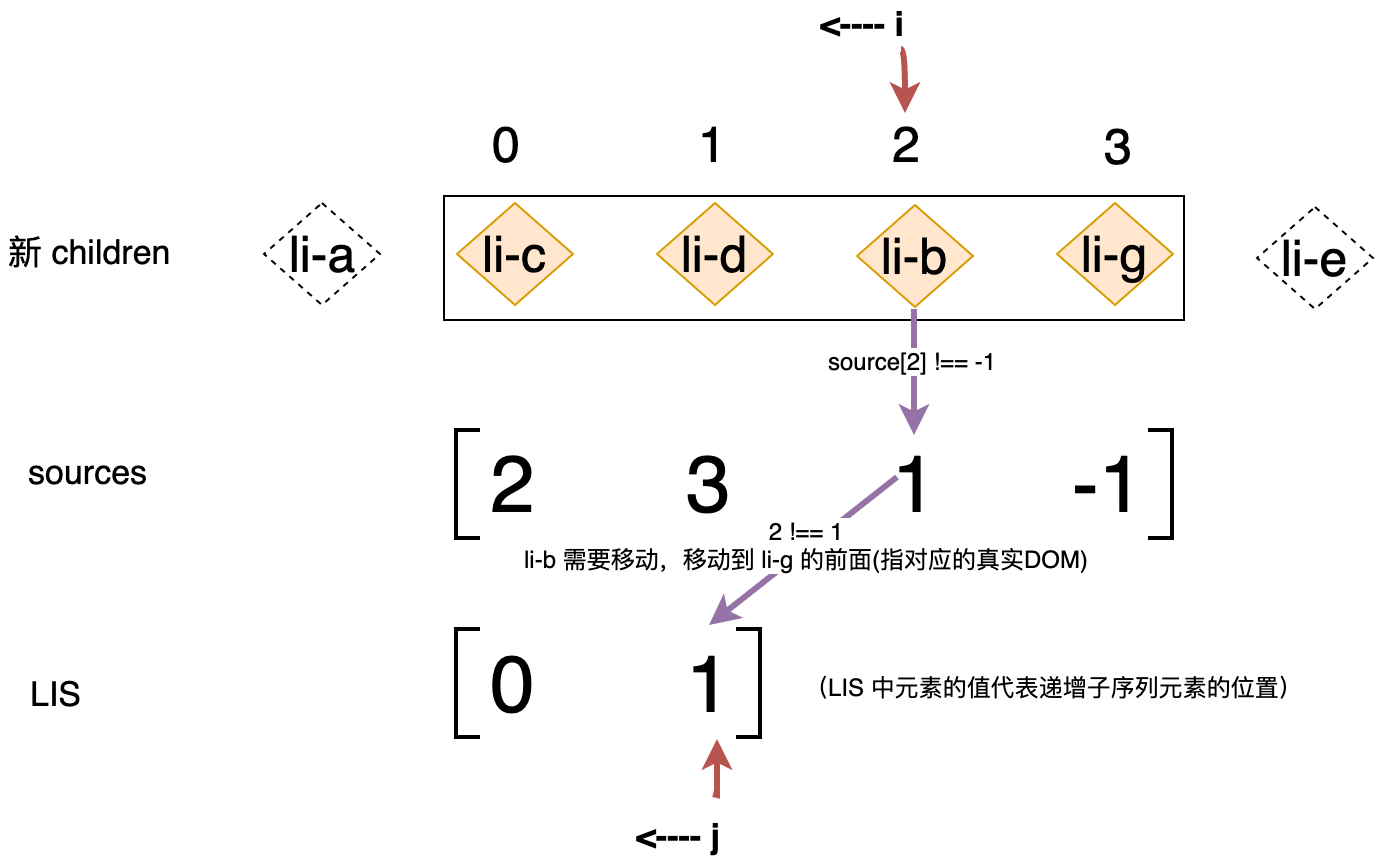
li-b 节点的位置索引 i 的值为 2,由于 source[2] 的值为 1,不等于 -1,说明 li-b 节点不是全新的节点。接着会判断 i !== seq[j],很显然 2 !== 1,这说明 li-b 节点是需要被移动的节点,那么应该如何移动呢?很简单,找到 li-b 节点的后一个节点(li-g),将其插入到 li-g 节点的前面即可,由于 li-g 节点已经被挂载,所以我们能够拿到它对应的真实 DOM,如下高亮代码所示:
if (moved) {
const seq = lis(source)
// j 指向最长递增子序列的最后一个值
let j = seq.length - 1
// 从后向前遍历新 children 中的剩余未处理节点
for (let i = nextLeft - 1; i >= 0; i--) {
if (source[i] === -1) {
// 作为全新的节点挂载
// 该节点在新 children 中的真实位置索引
const pos = i + nextStart
const nextVNode = nextChildren[pos]
// 该节点下一个节点的位置索引
const nextPos = pos + 1
// 挂载
mount(
nextVNode,
container,
false,
nextPos < nextChildren.length
? nextChildren[nextPos].el
: null
)
} else if (i !== seq[j]) {
// 说明该节点需要移动
// 该节点在新 children 中的真实位置索引
const pos = i + nextStart
const nextVNode = nextChildren[pos]
// 该节点下一个节点的位置索引
const nextPos = pos + 1
// 移动
container.insertBefore(
nextVNode.el,
nextPos < nextChildren.length
? nextChildren[nextPos].el
: null
)
} else {
// 当 i === seq[j] 时,说明该位置的节点不需要移动
// 并让 j 指向下一个位置
j--
}
}
}
到了这里 li-b 节点已经被我们移动到了正确的位置,接着会进行下一次循环,如下图所示:
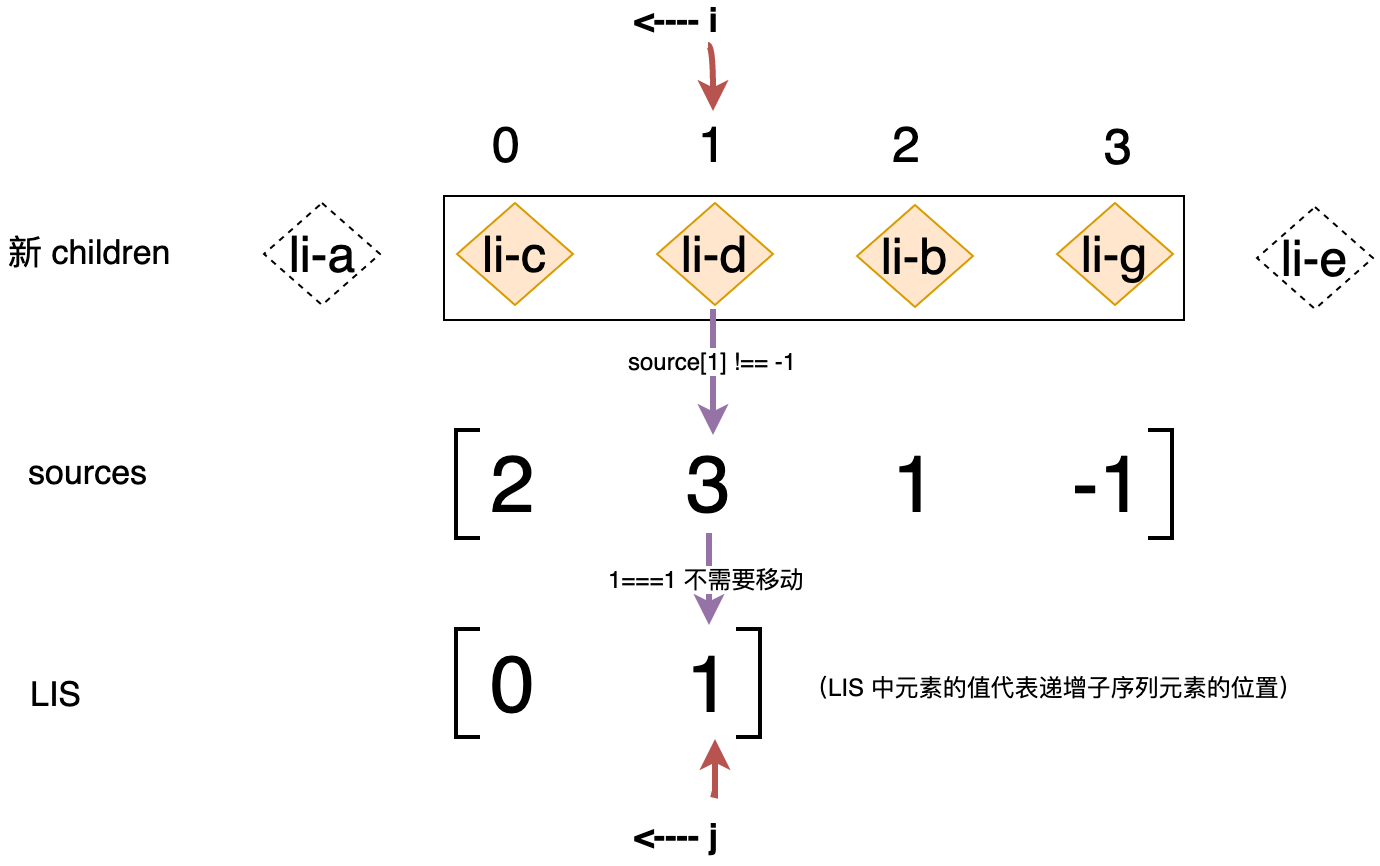
此时索引 j 依然指向子序列的最后一个位置,索引 i 的值为 1,它指向 li-d 节点。同样的,由于 source[1] 的值为 3 不等于 -1,说明 li-d 节点也不是全新的节点。接着判断 li-d 节点的位置索引 i 的值与子序列 seq[j] 的值相等,都为 1,这说明 li-d 节点不需要被移动,此时会把索引 j 指向下一个位置,结束本次循环并开启下一次循环,下一次循环时的状态如下图所示:
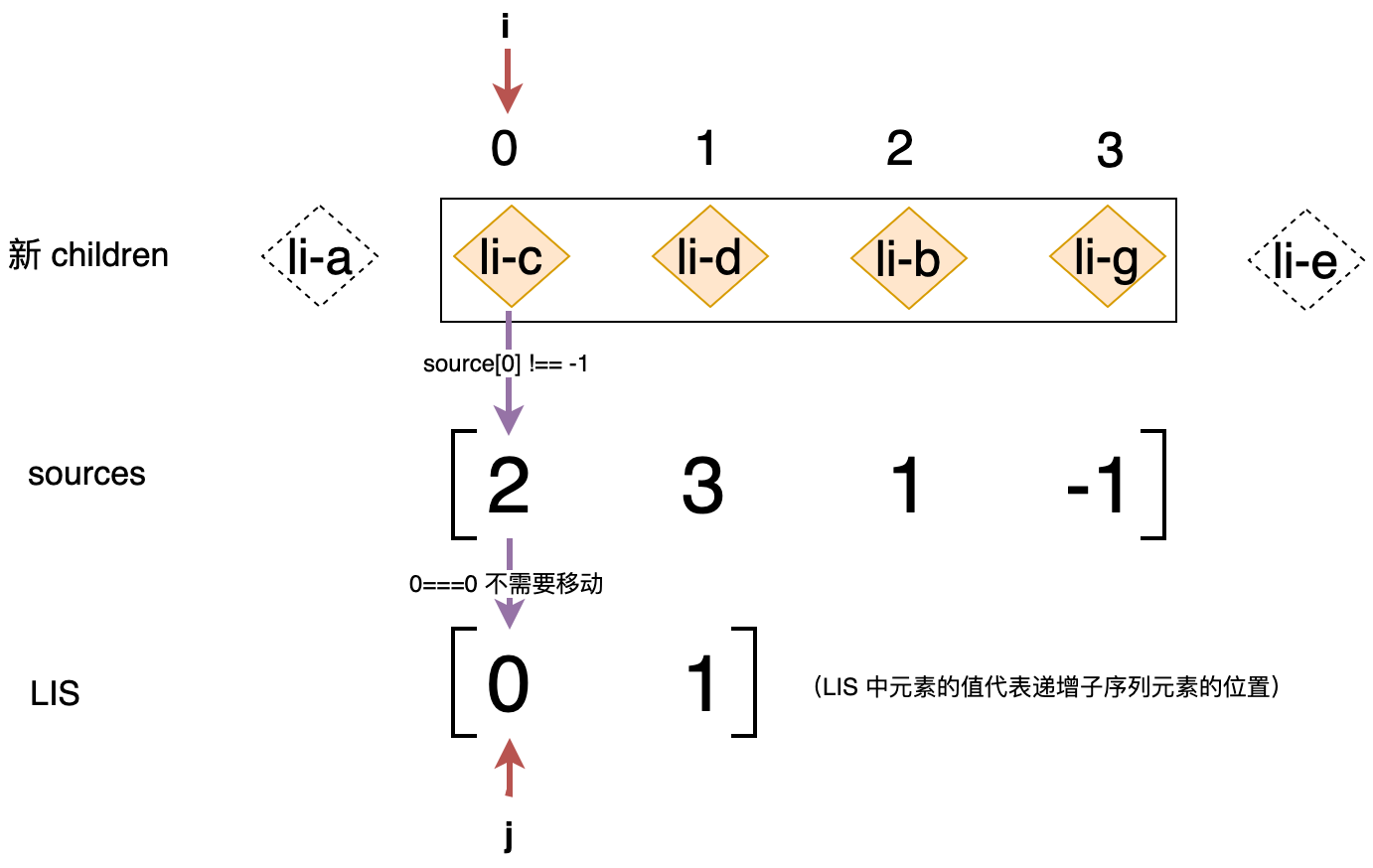
li-c 节点既不是新节点,也不需要被移动,至此循环结束,更新完成。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/4lrqpv0jm9 (opens new window)
# 求解最长递增子序列
上一小节我们已经介绍了什么是最长递增子序列,同时我们使用 lis 函数求解一个给定序列的最长递增子序列,本节我们就来探索一下如何求出给定序列的最长递增子序列。
设给定的序列如下:
[ 0, 8, 4, 12, 2, 10 ]
实际上,这是一个可以利用动态规划思想求解的问题。动态规划的思想是将一个大的问题分解成多个小的子问题,并尝试得到这些子问题的最优解,子问题的最优解有可能会在更大的问题中被利用,这样通过小问题的最优解最终求得大问题的最优解。那么对于一个序列而言,它的子问题是什么呢?很简单,序列是有长度的,所以我们可以通过序列的长度来划分子问题,如上序列所示,它有 6 个元素,即该序列的长度为 6,所以我们可不可以将这个序列拆解为长度更短的序列呢?并优先求解这些长度更短的序列的最长递增子序列,进而求得原序列的最长递增子序列?答案是肯定的,假设我们取出原序列的最后一个数字单独作为一个序列,那么该序列就只有一个元素:[ 10 ],很显然这个只有一个元素的序列的长度为 1,已经不能更短了。那么序列 [ 10 ] 的最长递增子序列是什么呢?因为只有一个元素,所以毫无递增可言,但我们需要一个约定:当一个序列只有一个元素时,我们认为其递增子序列就是其本身,所以序列 [ 10 ] 的最长递增子序列也是 [ 10 ],其长度也是 1。
接着我们将子问题进行扩大,现在我们取出原序列中的最后两个数字作为一个序列,即 [ 2, 10 ]。对于这个序列而言,我们可以把它看作是由序列 [ 2 ] 和序列 [ 10 ] 这两个序列所组成的。并且我们观察这两个序列中的数字,发现满足条件 2 < 10,这满足了递增的要求,所以我们是否可以认为序列 [ 2, 10 ] 的最长递增子序列等于序列 [ 2 ] 和序列 [ 10 ] 这两个序列的递增子序列“之和”?答案是肯定的,而且庆幸的是,我们在上一步中已经求得了序列 [ 10 ] 的最长递增子序列的长度是 1,同时序列 [ 2 ] 也是一个只有一个元素的序列,所以它的最长递增子序列也是它本身,长度也是 1,最后我们将两者做和,可知序列 [ 2, 10 ] 的最长递增子序列的长度应该是 1 + 1 = 2。实际上我们一眼就能够看得出来序列 [ 2, 10 ] 的最长递增子序列也是 [ 2, 10 ],其长度当然为 2 啦。
为了不过于抽象,我们可以画出如下图所示的格子:
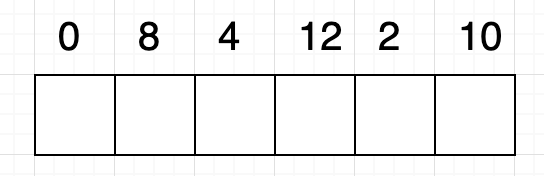
我们为原序列中的每个数字分配一个格子,并且这些格子填充 1 作为初始值:
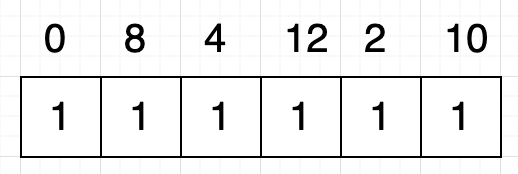
根据前面的分析,我们分别求得子问题的序列 [ 10 ] 和 [ 2, 10 ] 的最长递增子序列的长度分别为 1 和 2,所以我们修改对应的格子中的值,如下:
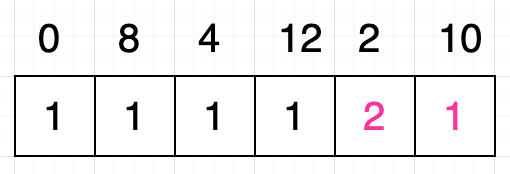
如上图所示,原序列中数字 10 对应的格子的值依然是 1,因为序列 [ 10 ] 的最长递增子序列的长度是 1。而原序列中数字 2 对应的格子的值为 2,这是因为序列 [ 2, 10 ] 的最长递增子序列的长度是 2。所以你应该发现了格子中的值所代表的是以该格子所对应的数字为开头的递增子序列的最大长度。
接下来我们继续扩大子问题,我们取出原序列中的最后三个数字作为子问题的序列:[ 12, 2, 10 ]。同样的,对于这个序列而言,我们可以把它看作是由序列 [ 12 ] 和序列 [ 2, 10 ] 这两个序列所组成的。但是我们发现条件 12 < 2 并不成立,这说明什么呢?实际上这说明:以数字 12 开头的递增子序列的最大长度就 等于 以数字 2 开头的递增子序列的最大长度。这时我们不需要修改原序列中数字 12 所对应的格子的值,如下图所示该格子的值仍然是 1:
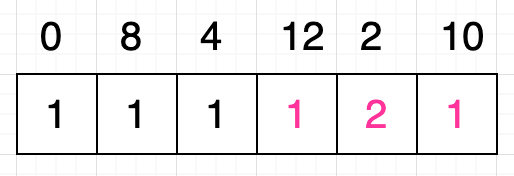
但是这就结束了吗?还不行,大家思考一下,刚刚我们的判断条件是 12 < 2,这当然是不成立的,但大家不要忘了,序列 [ 12, 2, 10 ] 中数字 2 的后面还有一个数字 10,我们是否要继续判断条件 12 < 10 是否成立呢?当然有必要,道理很简单,假设我们的序列是 [ 12, 2, 15 ] 的话,你会发现,如果仅仅判断条件 12 < 2 是不够的,虽然数字 12 不能和数字 2 构成递增的关系,但是数字 12 却可以和数字 15 构成递增的关系,因此我们得出当填充一个格子的值时,我们应该拿当前格子对应的数字逐个与其后面的所有格子对应的数字进行比较,而不能仅仅与紧随其后的数字作比较。按照这个思路,我们继续判断条件 12 < 10 是否成立,很显然是不成立的,所以原序列中数字 12 对应的格子的值仍然不需要改动,依然是 1。
接着我们进一步扩大子问题,现在我们抽取原序列中最后的四个数字作为子问题的序列:[ 4, 12, 2, 10 ]。还是同样的思路,我们可以把这个序列看作是由序列 [ 4 ] 和序列 [ 12, 2, 10 ] 所组成的,又因为条件 4 < 12 成立,因此我们可以认为子问题序列的最长递增子序列的长度等于序列 [ 4 ] 的最长递增子序列的长度与以数字 12 开头的递增子序列的最大长度之和,序列 [ 4 ] 的最长递增子序列的长度很显然是 1,而以数字 12 开头的递增子序列的最大长度实际上就是数字 12 对应的格子中的数值,我们在上一步已经求得这个值是 1,因此我们修改数字 4 对应的格子的值为 1 + 1 = 2:
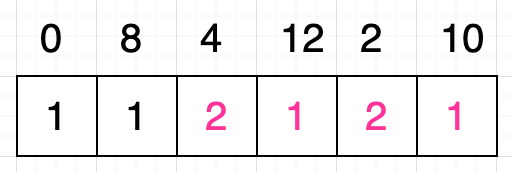
当然了,着同样还没有结束,我们还要判断条件 4 < 2 和 4 < 10 是否成立,原因我们在前面已经分析过了。条件 4 < 2 不成立,所以什么都不做,但条件 4 < 10 成立,我们找到数字 10 对应的格子中的值:1,将这个值加 1 之后的值为 2,这与现在数字 4 对应的格子中的值相等,所以也不需要改动。
到现在为止,不知道大家发现什么规律没有?如何计算一个格子中的值呢?实际很简单,规则是:
- 1、拿该格子对应的数字
a与其后面的所有格子对应的数字b进行比较,如果条件a < b成立,则用数字b对应格子中的值加1,并将结果填充到数字a对应的格子中。 - 2、只有当计算出来的值大于数字
a所对应的格子中的值时,才需要更新格子中的数值。
有了这两条规则,我们就很容易填充剩余格子的值了,接下来我们来填充原序列中数字 8 所对应的格子的值。按照上面的分析,我们需要判断四个条件:
8 < 48 < 128 < 28 < 10
很显然条件 8 < 4 不成立,什么都不做;条件 8 < 12 成立,拿出数字 12 对应格子中的值:1,为这个值再加 1 得出的值为 2,大于数字 8 对应格子的当前值,所以更新该格子的值为 2;条件 8 < 2 也不成立,什么都不做;条件 8 < 10 成立,拿出数字 10 对应格子中的值 1,为这个值再加 1 得出的值为 2,不大于数字 8 所对应格子中的值,所以什么都不需要做,最终我们为数字 8 所对应的格子填充的值是 2:
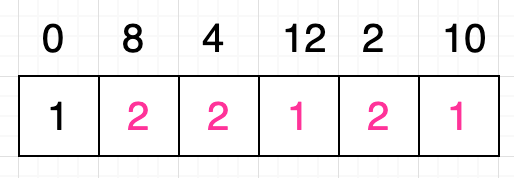
现在,就剩下原序列中数字 0 对应的格子的值还没有被更新了,按照之前的思路,我们需要判断的条件如下:
0 < 80 < 40 < 120 < 20 < 10
条件 0 < 8 成立,拿出数字 8 对应格子中的值 2,为这个值再加 1 得出的值为 3,大于数字 0 对应格子的当前值,所以更新该格子的值为 3。重复执行上面介绍的步骤,最终原序列中数字 0 对应格子的值就是 3:
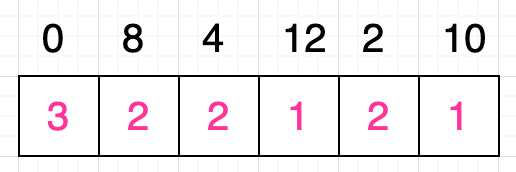
如上图所示,现在所有格子的值都已经更新完毕,接下来我们要做的就是根据这些值,找到整个序列的最长递增子序列。那么应该如何寻找呢?很简单,实际上这些格子中的最大值就代表了整个序列的递增子序列的最大长度,上图中数字 0 对应格子的值为 3,是最大值,因此原序列的最长递增子序列一定是以数字 0 开头的:
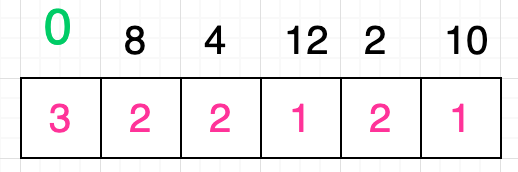
接着你需要在该值为 3 的格子后面的所有格子中寻找数值等于 2 的格子,你发现,有三个格子满足条件,分别是原序列中数字 8、4、2 所对应的格子。假设你选取的是数字 4:
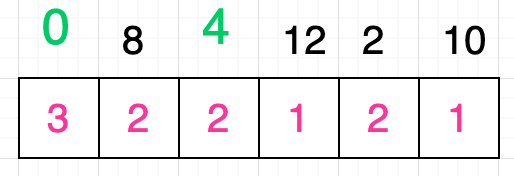
同样的,你需要继续在数字 4 对应的格子后面的所有格子中寻找到数值为 1 的格子,你发现有两个格子是满足条件的,分别是原序列中数字 12 和数字 10 所对应的格子,我们再次随机选取一个值,假设我们选择的是数字 10:
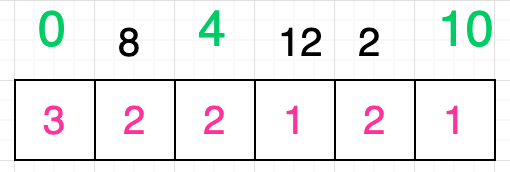
由于格子中的最小值就是数字 1,因此我们不需要继续寻找了。观察上图可以发现,我们选取出来的三个数字其实就是原序列的最长递增子序列:[ 0, 4, 10 ]。当然,你可能已经发现了,答案并非只有一个,例如:
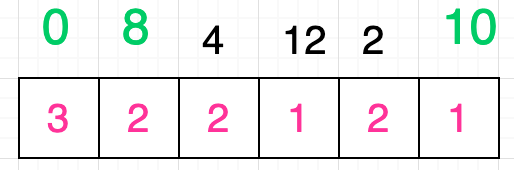
关键在于,有三个格子的数值是 2,因此你可以有三种选择:
[ 0, 8 ][ 0, 4 ][ 0, 2 ]
当你选择的是 [ 0, 8 ] 时,又因为数字 8 对应的格子后面的格子中,有两个数值为 1 的格子可供选择,所以你还有两种选择:
[ 0, 8, 12 ][ 0, 8, 10 ]
同样的,如果你选择的是 [ 0, 4 ],也有两个选择:
[ 0, 4, 12 ][ 0, 4, 10 ]
但当你选择 [ 0, 2 ] 时,你就只有一个选择:
[ 0, 2, 10 ]
这是因为数字 2 所对应的格子后面,只有一个格子的数值是 1,即数字 10 所对应的那个格子,因此你只有一种选择。换句话说当你选择 [ 0, 2 ] 时,即使数字 12 对应的格子的值也是 1,你也不能选择它,因为数字 12 对应的格子在数字 2 对应的格子之前。
以上,就是我们求得给定序列的所有最长递增子序列的算法。
TIP
上面的讲解中我们优先选择数值为 3 的格子,实际上我们也可以从小往大的选择,即先选择数值为 1 的格子,道理是一样。
TIP
完整代码&在线体验地址:https://codesandbox.io/s/32wjmo7omq (opens new window)
# 不足之处
实际上,我们确实花费了很大的篇幅来尽可能全面的讲解 Virtual DOM 核心的 Diff 算法,然而这里面仍然存在诸多不足之处,例如我们在移除一个 DOM 节点时,直接调用了 Web 平台的 removeChild 方法,这是因为在以上讲解中,我们始终假设新旧 children 中的 VNode 都是真实 DOM 的描述,而不包含组件的描述或其他类型 VNode 的描述,但实际上 children 中 VNode 的类型可以是任意的,因此我们不能简单的通过 Web 平台的 removeChild 方法进行 DOM 移除操作。这时我们需要封装一个专用函数:removeVNode,该函数专门负责移除一个 VNode,它会判断该 VNode 的类型,并采用合适的方式将其所渲染的真实 DOM 移除。大家思考一下,如果将要被移除的 VNode 是一个组件的描述,那是否还应该在移除之前或之后分别调用 beforeUnmount 以及 unmounted 等生命周期钩子函数呢?答案当然是肯定的。不过,本节讲解的内容虽然存在不足,但至少思路是完全正确的,在此基础上,你可以发挥自己的想象或者结合真正 Vue3 的源码去进一步的提升。